Solving an ODE with the Laplace transform

[PainterGuy]

Hi again,

The previous problem was done using y′′(t)+2y′(t)+10y(t)=10 with with intial condition y(0⁻)=0.

In the following case, I'm using an initial condition and setting the right hand side equal to zero.

Find y(t) for the following differential equation with intial condition y(0⁻)=4.
y′′(t)+2y′(t)+10y(t)=0

Using the following formulas.
ℒy(t)=Y(s)
ℒ{y′(t)}=sY(s)-f(0⁻)=sY(s)-4
ℒ{y′′(t)}=ℒ{(sY(s)-4)′}=ℒ{(sY(s)′-4′)}=ℒ{(sY(s)′)}=s²Y(s)-4s

y′′(t)+2y′(t)+10y(t)=0
⇒{s²Y(s)-4s}+2{sY(s)-4}+10Y(s)=0
⇒s²Y(s)-4s+2sY(s)-8+10Y(s)=0
⇒s²Y(s)+2sY(s)+10Y(s)-4s-8=0
⇒s²Y(s)+2sY(s)+10Y(s)=4s+8
⇒Y(s){s²+2s+10}=4s+8
⇒Y(s) = (4s+8) / (s²+2s+10)

Now finding the inverse Laplace transform.

Method 1:
https://www.physicsforums.com/attac...261154/?hash=ab39a4f0474f3384a6a5c37cdc441e05

Method 2:
This method I found from this video.

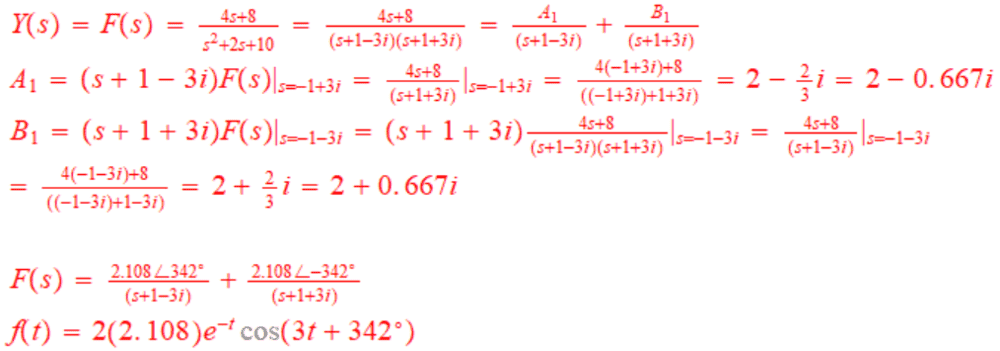
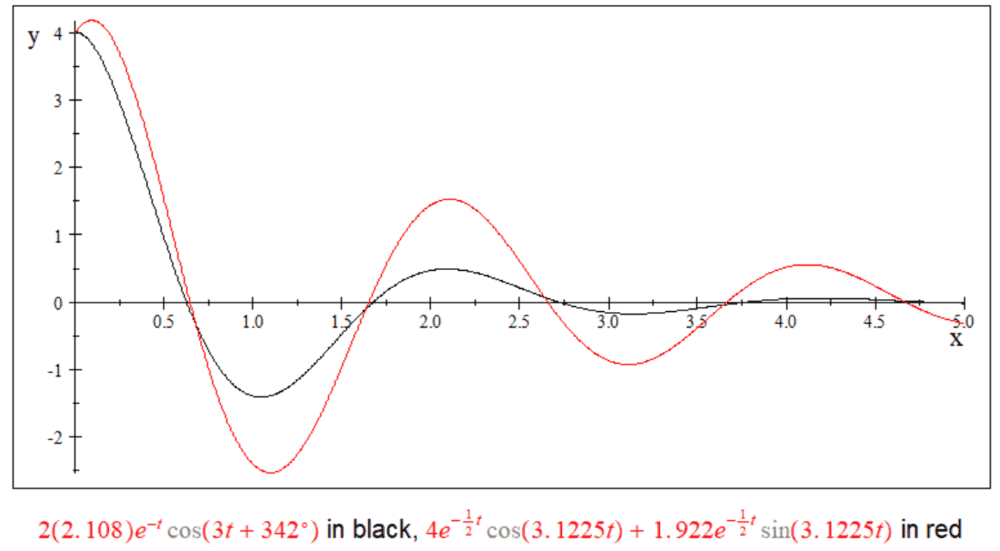
Question:
You can see that I'm getting different functions, f(t), for the mentioned methods. Where am I going wrong? Which f(t) is correct? Thank you for the help.

 

[Mark44]

For a 2nd-order DE, you need two initial conditions, typically f(0) and f'(0).
This formula from above isn't correct:

ℒ{y′′(t)}=ℒ{(sY(s)-4)′}=ℒ{(sY(s)′-4′)}=ℒ{(sY(s)′)}=s²Y(s)-4s

See #36 in this table: http://tutorial.math.lamar.edu/pdf/Laplace_Table.pdf

 

[vela]

In your first attempt, you complete the square incorrectly: $s^2+2s+10 = (s+1)^2+9$.

 

[PainterGuy]

For a 2nd-order DE, you need two initial conditions, typically f(0) and f'(0).
This formula from above isn't correct:

Thank you. Yes, sorry, I didn't realize it at that time.

The previous problem was done using y′′(t)+2y′(t)+10y(t)=10 with with intial condition y(0⁻)=0. If y(t) represents displacement then its first derivative would be velocity function, v(t). As an initial condition it is assumed that y'(0⁻)=v(0⁻)=0. Now we have two initial conditions, i.e. two pieces of information about the system just a moment before it's analytically observed.

In your first attempt, you complete the square incorrectly: $s^2+2s+10 = (s+1)^2+9$.

I have corrected Method 1 below. Now the results from both Methods agree. But I have a related question which is below the plot.

Question:
Apparently I completed the square wrongly but overall my completed square agrees with the original expression s²+2s+10. So, does completing a square method require that no fractions or decimals should be used, or what else is wrong with my method? Please guide me.

s²+2αs+α²+β²=s²+2s+10=s²+2(1/2)s+(1/2)²+(3.1225)²={s+(1/2)}²+3.1225²=(s+α)²+β²

 

[vela]

s²+2(1/2)s+(1/2)²+(3.1225)²

Without assuming what the answer is, try simplifying that expression. I guarantee you do not get what you started with.

 

[PainterGuy]

Let's try it: s²+2(1/2)s+(1/2)²+(3.1225)² =s²+(2/2)s+(1/4)+9.750=s²+s+0.25+9.750=s²+s+10

original expression: s²+2s+10

s²+2s+10 ≠ s²+s+10

Sorry!

 

[PainterGuy]

Hi,

I read somewhere that for a transfer function, the number of poles (roots of denominator) and zeros (roots of numerator) is equal. The transfer function from post #1, Y(s)=(4s+8) / (s²+2s+10), has poles at -1±3i and a zero at -2. Where is the second zero located? Thank you for the help!

 

[PainterGuy]

Could someone please comment on my previous post?

 

[PainterGuy]

Original expression: Y(s)=(4s+8) / (s²+2s+10)

I think we could divide both numerator and denominator by "s²".

(1/s²)(4s+8) / (1/s²)(s²+2s+10) = (4/s+8/s²) / (1+2/s+10/s²)

As s→∞ (4/s+8/s²) / (1+2/s+10/s²) = 0/1 = 0

I think it gives us a zero at infinity.