SUMMARY
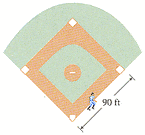
The discussion focuses on the geometry of a baseball diamond, specifically analyzing the distances and speeds involved when a batter runs from home plate to first base. The batter runs at a speed of 25 ft/s, and the problem requires calculating the rate at which his distance from second base decreases when he is halfway to first base, as well as the rate at which his distance from third base increases at that moment. The calculations involve applying principles of related rates in calculus.
PREREQUISITES
- Understanding of basic geometry, specifically the properties of squares.
- Familiarity with calculus concepts, particularly related rates.
- Knowledge of the Pythagorean theorem for distance calculations.
- Ability to set up and solve differential equations.
NEXT STEPS
- Study related rates problems in calculus to enhance problem-solving skills.
- Learn how to apply the Pythagorean theorem in dynamic scenarios.
- Practice calculating rates of change in real-world contexts.
- Explore geometric interpretations of speed and distance in sports analytics.
USEFUL FOR
Students of calculus, mathematics educators, sports analysts, and anyone interested in the application of geometry and calculus in real-world scenarios, particularly in sports contexts.