Solving Calc Homework: Lifting a Chain to the Ceiling

[Jet1045]

Homework Statement

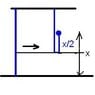
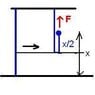
Alright, so my calc class isn't getting easier and we started doing 'work' problems, and I'm just not getting it. Here's the question: A 10ft long weighs 25l and hangs from a ceiling. Find the work done in lifting the lower end of the chain to the ceiling so that its level with the upper end.

Homework Equations

The Attempt at a Solution

Alright, so for the interval of [0,10] you would divide it into n subintervals of length Δx.
The weight of the piece would be (25/10)Δx which is simplified to (5/2)Δx

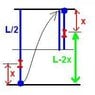
So in class we did an example similar to this but it only involved lifting the cable to the top of the roof, where as this question you are taking the bottom and lifting it to meet the other end at the roof. So i don't think it is as simple as taking the integral from 0 to 10 of (5/2)x like it is for just lifting a chain to the top of the roof.
ANy help would be greatly appreciated. :)

 

[ehild]

Hi Jet1045,

This thread should be placed to "Introductory Physics".

The best start to solve a Physics problem is drawing a picture. Do it. Show the piece of chain that you hold and move upward at some instant and find out the force needed to that, and the work done by lifting that piece by a small distance dx. Do the integration. What are the limits?
You also can use conservation of energy. Find out the gain of potential energy: it is equal to your work.

ehild

 

[Jet1045]

Oh, k sorry, I am doing it in my calc class so i assumed it would be here.

K that all helps, but then how is this question different than one where you just pull a chain straight to the roof?

 

[HallsofIvy]

This is a perfectly good question for the Calculus Math section. Jet1045, you are only lifting half of the chain. Further, you are not lifting all of the lower section to the top. If the chain has length L then the point at distance x above the bottom is lifted a distance L- 2x. Do you see why? (Draw a picture.)

 

[Jet1045]

This is a perfectly good question for the Calculus Math section. Jet1045, you are only lifting half of the chain. Further, you are not lifting all of the lower section to the top. If the chain has length L then the point at distance x above the bottom is lifted a distance L- 2x. Do you see why? (Draw a picture.)

OHHH! obviously, how did i not see that before. If you're lifting only the bottom to the roof then half of the chain won't move at all! Thanks so much. I'm going to try and work on it now :)

 

[Jet1045]

This is a perfectly good question for the Calculus Math section. Jet1045, you are only lifting half of the chain. Further, you are not lifting all of the lower section to the top. If the chain has length L then the point at distance x above the bottom is lifted a distance L- 2x. Do you see why? (Draw a picture.)

Oh wait, one quick question before i try it. How come it is L-2x and not just L-x?

 

[ehild]

You have to draw a picture, like the attached one.

ehild

 

[Jet1045]

thanks for all the help, but now I am more confused about the distance its moving.
i thought it would maybe be 10-x, hallsofivy you said L-2x (or 10-2x) and ehild what i am getting from your picture is x/2. I am so confused on which to use. Any clarity on this would be appreciated:)

 

[Jet1045]

NEVERMINDD! i got it haha
Thanks for everything :)

 

[ehild]

You can call "x" anything, but you have to define what it is. Make a picture and show it.

In my drawing, (the picture on the left), x is the height of the end of the thread at an instant, when lifted upward.

At a given instant, I hold the end, shown by the dot, at x height from the floor. The force I had to exert on the thread is equal to the weight of the piece hanging in my hand. It is (25/10)*x/2. When lifting that piece by dx, I do dW=Fdx=2.5(x/2)dx work. (Work is force times displacement.)

You need to calculate the integral

W=\int_0^L{1.25 x dx}

HallsofIvy had an other way of taught. See picture on the right.

x is the height of a piece of thread (shown in red) above the floor initially. After the bottom end of thread is lifted up to the ceiling the red piece will be at distance x below the ceiling. So it moved by 2L-x. You have to integrate for half of the length, as the upper half of the thread does not move.

ehild

 

[Jet1045]

oh thanks ehild for the clarification! i washaving a hard time imagining why it would be L-2x because i wasnt realising that the distance at a point from the bottom of the chain will be equal to the distance to the roof from that same point once the bottom fot he chain touches the roof.
thanks again!

 

[ehild]

Next time start with a picture. Imagine the situation and draw it. ehild