HansBu
- 24
- 5
- Homework Statement
- Hello everyone! I am having some confusions with regards to my problem, whether or not the differential equations presented to me are inclined to damped driven pendulum. From the differential equations given, I can see that these equations are part of the convection equations made my Lorenz dubbed as Lorenz equations.
- Relevant Equations
- The relevant equations are presented in the attempt to the solution part.
Here are the nonlinear and coupling ordinary differential equations:
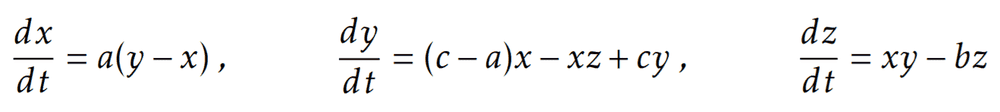
I was given values of a, b, and c as well as some initial values for x, y, and z. If ever the equations above are related to the pendulum, I can think of a as the damping factor, b as the forcing amplitude, and c as the driving frequency. On the other hand, initial values of x and y represent initial angular displacement and initial angular velocity, respectively. Can you help me verify this thought of mine? I have gone through a lot of resources and I am now confused. I am hoping that this forum might clear any confusions I have on mind. Thank you so much! A sample output shown below might be a help.
NOTE: I was able to come up with the source code in order to print out the graph below. My only concern here is the concept behind it.
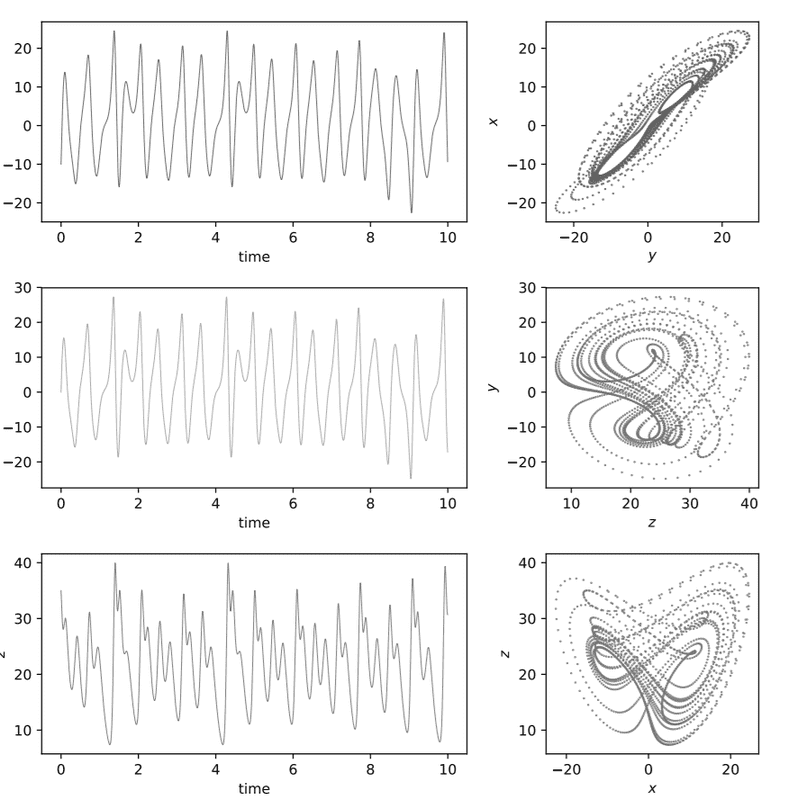
I was given values of a, b, and c as well as some initial values for x, y, and z. If ever the equations above are related to the pendulum, I can think of a as the damping factor, b as the forcing amplitude, and c as the driving frequency. On the other hand, initial values of x and y represent initial angular displacement and initial angular velocity, respectively. Can you help me verify this thought of mine? I have gone through a lot of resources and I am now confused. I am hoping that this forum might clear any confusions I have on mind. Thank you so much! A sample output shown below might be a help.
NOTE: I was able to come up with the source code in order to print out the graph below. My only concern here is the concept behind it.