- #1
qumbo19
- 7
- 1
Thread moved from the technical forums to the schoolwork forums
TL;DR Summary: I am doing an experiment for my Physics IA and don't know the theory behind it
I am working on a Physics experiment for my school where I vary the distance between a simple pendulum and an aluminium block, and get the damping coefficient for each distance. Below are the images of the setup and the data I collected:
Image of setup:

Image of data:
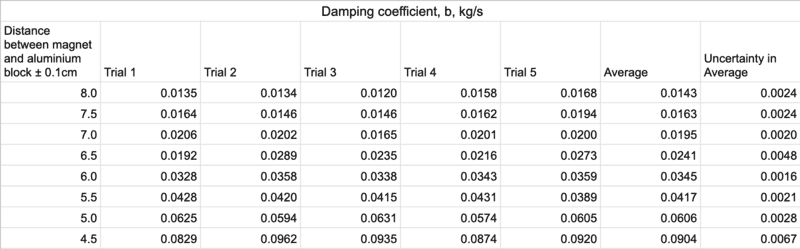
As you can see from the setup, I use some glass to raise the height of the aluminium block in increments. I know the theory is that the eddy currents somehow oppose the motion of the pendulum and thus causes the damping, but I can't find any equations that connect the two. What graph can I do to obtain some values related to the setup? I can't find much theory on this experiment and would really appreciate some help on this! I have tried finding the relationship between the two: by b = k d^n. Where k and n are constants to be found, b is damping coefficient and d is distance, and then I log both sides and find them from the gradient and intercept. But I don't even know if this is a valid approach.
I am working on a Physics experiment for my school where I vary the distance between a simple pendulum and an aluminium block, and get the damping coefficient for each distance. Below are the images of the setup and the data I collected:
Image of setup:

Image of data:
As you can see from the setup, I use some glass to raise the height of the aluminium block in increments. I know the theory is that the eddy currents somehow oppose the motion of the pendulum and thus causes the damping, but I can't find any equations that connect the two. What graph can I do to obtain some values related to the setup? I can't find much theory on this experiment and would really appreciate some help on this! I have tried finding the relationship between the two: by b = k d^n. Where k and n are constants to be found, b is damping coefficient and d is distance, and then I log both sides and find them from the gradient and intercept. But I don't even know if this is a valid approach.
Last edited by a moderator: