archaic
- 688
- 214
- Homework Statement
- $$\epsilon^\frac32=\mu^\frac32+\frac{\left(\pi k_B T\right)^2}{8}\frac1{\mu^\frac12}$$
I am given that ##\epsilon\approx\mu## and ##(1+x)^\alpha\approx1+\alpha x## when ##x\to0##.
- Relevant Equations
- ##(1+x)^\alpha\approx1+\alpha x## when ##x\to0##
I have tried manipulating this to
$$1-\frac{8}{(\pi k_B T)^2}\mu^\frac12(\epsilon^\frac32-\mu^\frac32)=0\Leftrightarrow\left[1+\mu^\frac12(\epsilon^\frac32-\mu^\frac32)\right]^{-\frac{8}{(\pi k_B T)^2}}=0$$
but this doesn't seem to lead anywhere.
any hints please?
the solution is one of these ##T_f=\epsilon/k_B##:
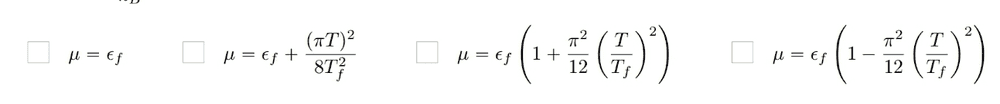
$$1-\frac{8}{(\pi k_B T)^2}\mu^\frac12(\epsilon^\frac32-\mu^\frac32)=0\Leftrightarrow\left[1+\mu^\frac12(\epsilon^\frac32-\mu^\frac32)\right]^{-\frac{8}{(\pi k_B T)^2}}=0$$
but this doesn't seem to lead anywhere.
any hints please?
the solution is one of these ##T_f=\epsilon/k_B##: