Solving for Guy Wires using the Law of Cosines - 100ft Tower on a Hill

[gabrielh]

Homework Statement

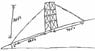
A 100-foot vertical tower is to be erected on the side of a hill that makes a 6^{\circ} angle with the horizontal. Find the length of each of the two guy wires that will be anchored 65 feet uphill and downhill from the base of the tower.

Homework Equations

Law of Cosines

a^{2} = b^{2} + c^{2} - (2bc)cos(a)
b^{2} = a^{2} + c^{2} - (2ac)cos(b)
c^{2} = a^{2} + b^{2} - (2ab)cos(c)

I included an sketched version of the image that was provided with this problem. Please forgive the sub par drawing skills.

The Attempt at a Solution

With a bit of help getting started and finding a couple of the unknown angles, I should be able to work this problem easily. I understand law of cosines quite well, I'm just unsure of the best way to begin this problem.

 

[jegues]

Hmmm... You could try splitting your building in half and creating two triangles.

Is it safe to assume the building is perpendicular to the plane?

 

[gabrielh]

Hmmm... You could try splitting your building in half and creating two triangles.

Is it safe to assume the building is perpendicular to the plane?

I'm not sure. That image and the problem statement is all I've been given.

 

[jegues]

Well in the image, is the building going striaght up vertically? Or is it tilted a bit, vertical to the plane?

 

[gabrielh]

Well in the image, is the building going striaght up vertically? Or is it tilted a bit, vertical to the plane?

Straight up vertically I believe would be safe to assume.

 

[jegues]

Well if the plane on which the structure stood was flat, then we could say that the angle in each triangle is simply 90, but since the plane is elevated by 6 degrees we can see that first triangle is going to take the 6 degree elevation and the second triangle will lose 6 degrees.

That should be enough to apply law of cosine or even use sine law to solve everything.

EDIT: That's just my thought process, I'd like someone to confrim my thoughts ;)

 

[Mentallic]

Yes that's how you'll find the angles between the tower and the cliff sloping up and down. But this is a cosine law problem, using the sine law will be quite more difficult and unnecessary since you'll have to find another angle in each triangle.

 

[jegues]

this is a cosine law problem, using the sine law will be quite more difficult and unnecessary since you'll have to find another angle in each triangle.

I agree the cosine law would be the better route to take in solving this problem.

 

[gabrielh]

Thanks for the help :)