smr101
- 72
- 0
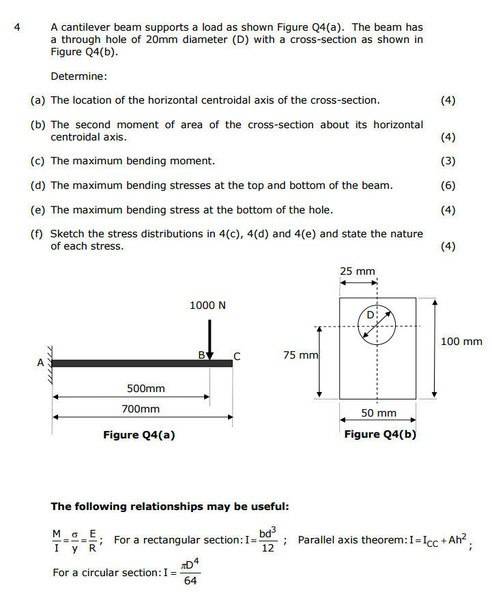
Hi, having problems with (a) here, I'll show my attempt:
A1 = (0.025 * 0.05) - ((pi*0.01^2)/ 2)
1.093 x10^-3 m^2
A2 = (0.075 * 0.05) - ((pi*0.01^2)/2)
= 3.593 x10^-3 m^2
A(total)*y(horz centroidal axis) = A1y1 + A2y2
y = 1.093 x10^-3 * 0.0875 + 3.593x10^-3 * 0.0375 /(4.686x10^-3)
= 49.19 mm
Correct answer is 48.32 mm, any idea where I've gone wrong?
Thanks.
A1 = (0.025 * 0.05) - ((pi*0.01^2)/ 2)
1.093 x10^-3 m^2
A2 = (0.075 * 0.05) - ((pi*0.01^2)/2)
= 3.593 x10^-3 m^2
A(total)*y(horz centroidal axis) = A1y1 + A2y2
y = 1.093 x10^-3 * 0.0875 + 3.593x10^-3 * 0.0375 /(4.686x10^-3)
= 49.19 mm
Correct answer is 48.32 mm, any idea where I've gone wrong?
Thanks.