Yankel
- 390
- 0
Hello all,
I need some help with this one, I do not have a clue how to even begin.
the level curve of
\[f(x,y)=x+4y^{2}\]
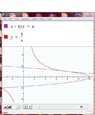
tangents the function
\[y=\frac{8}{x}\]
in a point at the first quarter. What is the tangent point, what is the equation of the level curve ?
This question need to involve implicit functions. I don't get it...
thanks !
I need some help with this one, I do not have a clue how to even begin.
the level curve of
\[f(x,y)=x+4y^{2}\]
tangents the function
\[y=\frac{8}{x}\]
in a point at the first quarter. What is the tangent point, what is the equation of the level curve ?
This question need to involve implicit functions. I don't get it...
thanks !