Solving IVP w/ Finite Difference: Strange Oscillations

[gstar2002]

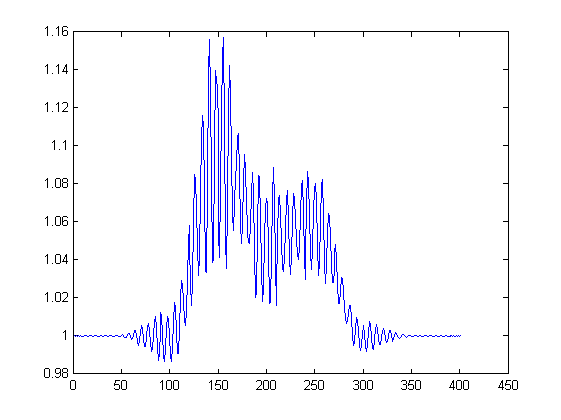
Hallo, I tried to use 'finite difference' method to solve a Initial Value Problem(IVP). For the two boundaries I used periodical condtion and for the differential operators I used 4th degree center approximations. But as result, I got this thing. Where comes this strange oscillation What do you think could be the problem. Should I use a smaller x stepsize? Will use a forward approximation help? Thanks.
Actually I am using matlab's odes15s.

update:
The strange thing is that, if I use a biger x stepsize, say 0.1, i will get a smooth result. With smaller stepsize from 0.08, I will get the result showed in the picture.
I tried ode45, which is based on an explicit Runge-Kutta (4,5) formula, the Dormand-Prince pair and ode23tb, which is an implementation of TR-BDF2. I got the same result.

Thanks.

\begin{aligned}
\dot{q} & = -\frac{\partial (6*q^2/5*h)}{\partial x}-\frac{3*q}{h^2}+h*h'''-(1+10*cos(pi*t))*h*h'\\
\end{aligned}

\begin{aligned}
\dot{h} & = -\frac{\partial q}{\partial x}
\end{aligned}

\begin{aligned}
h(t,0) = h(t,10),q(t,0) = q(t,10)
\end{aligned}


h(0,x), q(0,x) are known.
Thanks.

 

[jackmell]

I believe that's due to the stability of the method. See:

http://en.wikipedia.org/wiki/Von_Neumann_stability_analysis

Equation (10) of that gives the requirements on delta x and delta t for the method to be stable.