Solving LC circuit with energy conservation

[ermia]

Homework Statement

This is one of krotov's problems:
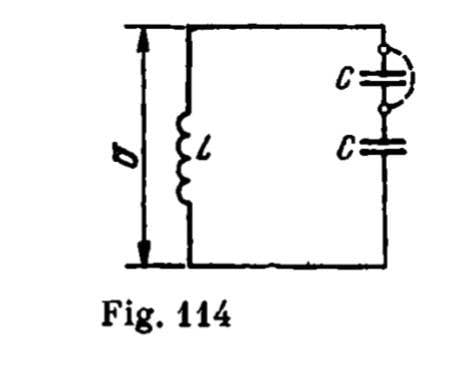
A bank of two series-connected capacitors
of capacitance C each is charged to a
voltage U and is connected to a coil of inductance L so that an oscillatory circuit
(Fig. 114) is formed at the initial moment.
After a time t, a breakdown occurs in one of
the capacitors, and the resistance between
its plates becomes zero.
Determine the amplitude of charge oscillations on the undamaged capacitor.

Relevant Equations

Equations of energy circuits
The frequency of LC circuits
etc.

krotovs solution is based on energy conservation. My question is that why the solution didn't consider inductors energy?
the question:

The solution:

 

[hutchphd]

Physically it is because the inductor energy depends only upon the current flowing through it. When the capacitor shorts out the current in the circuit is not immediately changed, except within the unfortunate (and now very warm) capacitor. The subsequent evolution of the current will change because the energy heated the now-shorted capacitor. Does that help?

 

[DaveE]

He must be assuming that the capacitor breakdown is much quicker than the response time of the LC resonator, so the inductor current doesn't change.

However, the phrase "the amplitude of charge oscillations after the breakdown" is confusing. The only oscillations in this circuit must include the inductor, RC circuits don't oscillate. To find the peak capacitor energy ("amplitude of charge oscillations"), you would have to include the inductor energy. Alternatively, you could just describe the charge on the capacitors immediately after the fast breakdown event, which should be zero for one and unchanged for the other (as I interpret his problem).

Yet another example of a poorly worded problem. I guess he's describing the nature of the initial transient and asking for the LC response following that event?

 

[kuruman]

My question is that why the solution didn't consider inductors energy?

Why do you say it didn't? The initial charge on the series combination is $q_0=C_{eq}U=\frac{1}{2}CU$. The initial energy stored in the capacitor is $E_0=\frac{1}{2}q_0U=\frac{1}{4}CU^2$. That energy does not change when the inductor is connected. At any time, the energy stored in the capacitor combination before breakdown is $E_C(t)=\frac{1}{4}CU^2\cos^2\omega_0 t=E_0\cos^2\omega_0 t$. Note that it is sometimes zero and sometimes $E_0$. When it's zero, all the energy is in the inductor; when it's $E_0$ all the energy is in the capacitors.

Krotov says, that the energy of the damaged capacitor at breakdown is half of $E_C(\tau)$ whatever that value is. The balance, $E_0-\frac{1}{2}E_C(\tau)$ is the energy left in the intact capacitor and the inductor. If the breakdown occurs when $\omega_0 \tau=\frac{2n+1}{2}\pi$ ($n$ = integer), all the energy is in the inductor and that is implicit in Krotov's equation for $W$.

 

[TSny]

You might find it worthwhile to think about the mechanical analog of this system: a mass-spring system with two parallel, massless springs and no friction:

The system is initially oscillating with ampltude $x_0$ such that $x(t) = x_0 \cos \omega t$.

At some arbitrary time $\tau$ one of the springs snaps so that only the other spring is operational.

Find the new amplitude of oscillation.