Solving Node Voltage: Va = Vb x R1/(R1+R0)

[385sk117]

Homework Statement

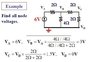
Find the node voltage

Homework Equations

Va = Vb x R1/(R1+R0)

The Attempt at a Solution

I didnt have the original picture of the question but this example is exactly same as the question that i had to solve. but I don't understand this thing from the first step.
How can Vb = Va x (4//4)/(4//4+2)? I know that the 2ohms at the right side of circuit can be added as series and functions as 4ohm and it is paralle to 4 ohm in the middle. and so the total resistance of the circuit is 4//4 +2, but why do we use 4//4 to find Vb? isn't it just 2ohm in front of Vb that we have to use?
Help please
Thanks

 

[hotvette]

What does the symbol // (as in 4 // 4) mean?

 

[kjohnson]

There are a lot of ways to analyze circuits and its been alittle while for me. That being said the easiest way to find Vb would be to find the resultant resistance of the right hand side/loop of the circuit. Since it turns out to be equal to 2 ohms then you have two resistors in series that are both 2 ohms. Thus the voltage drops will be equal to each other and be 1/2 of the source voltage or 3 volts.