How do I find Vth with the node voltage method?

[Purpleshinyrock]

Homework Statement

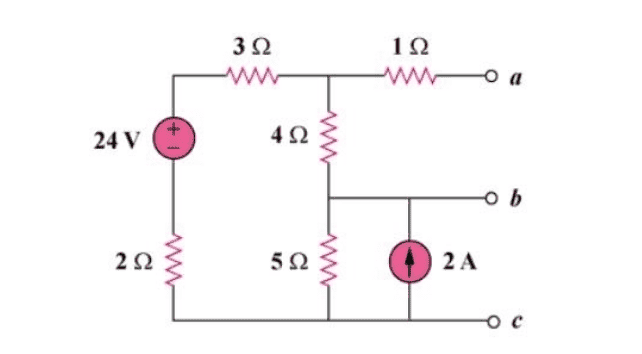
For the circuit in Fig. 4.111, obtain the Thevenin equivalent as seen from terminals (a) a-b (b) b-c

Relevant Equations

V=IR

Hello.
I'am practicing circuit analisis about the norton and thevenin's circuits and I can't seem to manage to get the right thevenin's voltage using the node voltage for a)

resolution
1) I did source transformation turning the current source(2A) into a voltage source (10V)
applied node voltage discarding the 1ohm resistance.
I got that Va=18V AND VB=10V
and since vth is in parallel with the 4 ohm resistance then: Vth=(Va-Vb)/4=2 but the solution says that Vth=4
Can you help me get to the desired result.
Your time and attention are deeply appreciated.
Thank you.

 

[Baluncore]

Try replacing voltage sources with short-circuits, and current sources with open-circuits.

 

[Purpleshinyrock]

Try replacing voltage sources with short-circuits, and current sources with open-circuits.

wouldn't it give me the Rth instead of the Vth?

 

[Baluncore]

Yes, sorry, I'm asleep.

 

[Baluncore]

When you inject 2 A into nodes b and c, you are NOT injecting it into the 5 R only. You are injecting it into the Rth between nodes b and c.

 

[Joshy]

It's been a while since I've used source transformation, but I tried it and it seemed to work great for me. I'm a little bit confused as to how you got V_A=18V and V_B=10V I'm assuming you are meaning this is respect to V_C=0V? I think it would be good if you can show a few steps of your work to show how you got to the 18V and 10V answer so that it will be easier to identify what went wrong. (I think I see what happened edited in below)

I'm assuming you already know that V_TH is the open circuit voltage, and so there's no current going through that 1 Ohm resistor- you did good there. You did your source transformation so that you have a 5 Ohm resistors and a 10 V source. That looks great to me! Now you have one big loop. What's the current going through that loop?

Once you have the current, then you will know what the voltage is across each resistor, and you can use that to solve for V_AB. Since it's one big loop and you have a few resistors in series with each other I think you'll be able to solve it no problem :) Something that might help you save some time after you solve for the current is to simply use V_B as your reference (ground) instead of V_C (if that's what you're doing). This way you can say "Okay, now that V_B is my reference all I need to know is the voltage across that 4 Ohm resistor (V times I) and I'm good"

edit:

Okay! I think I see what you did now that I've done a little fidgeting with it. It looks like to me you are assuming that after the source transformation, that the current going through your loop is still 2A. This is incorrect. This doesn't work. I'm not sure if that would work with only the current source in your system, but it definitely does not work here (there is another source in your system). Try solving for the current in your loop and you will see what happens.

 

[Baluncore]

Alternatively;
Make node c the ground reference. Reduce the resistor count to three.

Initially ignore the current source, then it is a simple voltage divider.
Calculate the voltage on node b due to the voltage source alone, Vbv = ?

Find the Thevenin equivalent resistance of node b relative to ground; Rthb = ?
Restore the current source and apply Ohms law to node b; Vbi = 2 amp * Rthb .
Then; Vb = Vbv + Vbi .

Now you have Vb and the 24 V source, so solve the upper voltage divider to find Va .

 

[Purpleshinyrock]

Alternatively;
Make node c the ground reference. Reduce the resistor count to three.

Initially ignore the current source, then it is a simple voltage divider.
Calculate the voltage on node b due to the voltage source alone, Vbv = ?

Find the Thevenin equivalent resistance of node b relative to ground; Rthb = ?
Restore the current source and apply Ohms law to node b; Vbi = 2 amp * Rthb .
Then; Vb = Vbv + Vbi .

Now you have Vb and the 24 V source, so solve the upper voltage divider to find Va .

Hello. Thank You for the reply.
I've tried to make node c the ground and go from there . can you tell me from the pdf bellow what I did wrong?

 

[Joshy]

Voltage above the 24V source is not 24V… it’s 24V above whatever the voltage below the voltage source is. It would be 24V if the voltage happened to be 0V or ground right there, but it is not if you are calling Va or Vb your ground.

I’m personally a little bit confused about this alternate recommendation because if you do it the way you were doing and the same way I recommended it becomes one big loop that is super easy to solve (don’t even need a voltage divider). I think what the person is recommending is a second thevenin equivalent circuit, which will work but is quite a bit of work compared to solving a single loop circuit. Please try the single loop circuit :) Do that current source to voltage source transformation and then tell me what is the current going through that loop? You can do it pretty easily with KVL you might even able to do it by inspection because you’re going to have a 24V supply and a 10V supply…. what does KVL tell you about the 14V difference of these two supplies? (big hint: The 14V is going across the resistors… so what is the current)

If you know what the current is then you will know what the voltage drop across that 4 Ohm resistor is using Ohm’s law and you’ll be done in a few seconds.

 

[Baluncore]

This is the simplified diagram.

The voltage on node b due to 24 V source; Vbv = 24V * 5 / ( 5 + 4 + 5 ) ;
Rthb = 5 // ( 4 + 5 ) ;
Vbi = 2 A * Rthb ;
Vb = Vbv + Vbi ;

 

[Joshy]

Ah I see superposition principle. No denying it's good to have an alternate way to solve or check the problem. OP was on the right track though. They made a bad assumption that 2A from the source transform would be the same current would be in the loop (but must have overlooked the current from the other source), which is why they incorrectly thought it was 18V and 10V (2A times 9 Ohms = 18V, and 2a times 5 Ohms = 10V); however if they solved for the current in the single loop they would be good to go.

To solve for the current it's a pretty straightforward KVL problem that can be done by inspection. They know that if they had a 24V and 10V source side by side it would be a contradiction unless there were some resistors that could help solve that problem. There is! So with 24V and a 10V source in this orientation it's very apparent that something has to happen with the 14V with some resistors that are in series, which is very convenient.