gnits
- 137
- 46
- Homework Statement
- To find the internal forces acting in a certain system
- Relevant Equations
- moments and equating of forces
Please could I ask with help with the following question:

I have done part (a) and agree with the answer given in the book of 2a (2w + w1) sin(Ө)
It is part (b) where I am stuck. Here is my diagram:
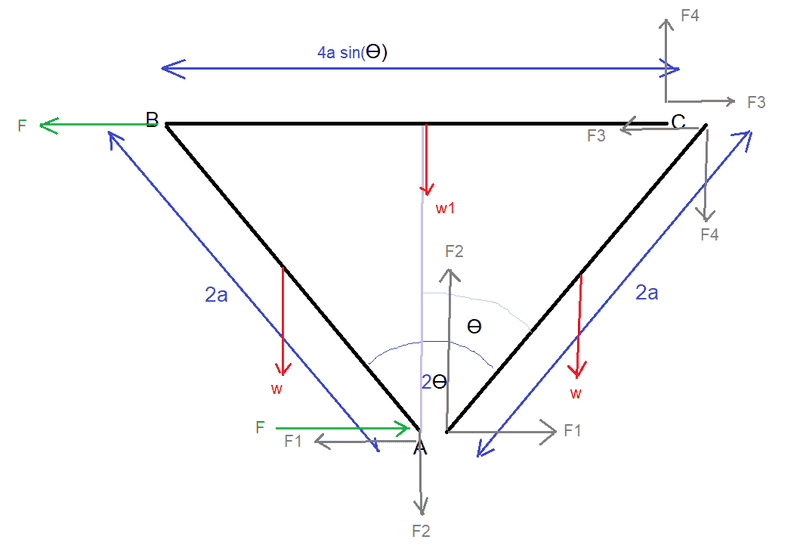
(In green are show the forces of the couple - but they are not needed in my following working)
In grey, I have labelled the internal forces F1, F2, F3 and F4 on the system when considered as being made up of the two parts ABC and AC.
I need to find F3, F4, F1 and F2.
I have these four answers from the book, they are:
(1/2)*(w + w1) tan(Ө)
(1/2)*w1
(1/2)*(w + w1) tan(Ө)
(1/2)*(2w + w1)
Considering rod AC only and resolving horizontally I have:
F3 = F1
and resolving vertically I have:
F2 = F4 + w
These equations are consistent with the given answers.
Still considering only rod AC, taking moments about A leads to:
2*F3 = w *tan(Ө) + 2 * F4 * tan(Ө)
(again, this is satisfied by the given answers)
And taking moments about C leads to:
2*F1 + w * tan(Ө) = 2 * F2 * tan(Ө)
(again, this is satisfied by the given answers)
So I have these four equations, which the required answers satisfy, but I can't see how to determine the values of F1, F2, F3 or F4 from these. I need another equation.
I thought to consider the part ABC and resolve vertically, but this leads to:
F4 = w + w1 + F2
Which is NOT satisfied by the required answers.
How can I proceed? (Have I labelled the internal forces with the correct directions?).
Thank for any help,
Mitch.
I have done part (a) and agree with the answer given in the book of 2a (2w + w1) sin(Ө)
It is part (b) where I am stuck. Here is my diagram:
(In green are show the forces of the couple - but they are not needed in my following working)
In grey, I have labelled the internal forces F1, F2, F3 and F4 on the system when considered as being made up of the two parts ABC and AC.
I need to find F3, F4, F1 and F2.
I have these four answers from the book, they are:
(1/2)*(w + w1) tan(Ө)
(1/2)*w1
(1/2)*(w + w1) tan(Ө)
(1/2)*(2w + w1)
Considering rod AC only and resolving horizontally I have:
F3 = F1
and resolving vertically I have:
F2 = F4 + w
These equations are consistent with the given answers.
Still considering only rod AC, taking moments about A leads to:
2*F3 = w *tan(Ө) + 2 * F4 * tan(Ө)
(again, this is satisfied by the given answers)
And taking moments about C leads to:
2*F1 + w * tan(Ө) = 2 * F2 * tan(Ө)
(again, this is satisfied by the given answers)
So I have these four equations, which the required answers satisfy, but I can't see how to determine the values of F1, F2, F3 or F4 from these. I need another equation.
I thought to consider the part ABC and resolve vertically, but this leads to:
F4 = w + w1 + F2
Which is NOT satisfied by the required answers.
How can I proceed? (Have I labelled the internal forces with the correct directions?).
Thank for any help,
Mitch.
Last edited: