Solving Pendulum Questions: Calculate Initial PE & KE

In summary, the conversation is about calculating the starting height and potential energy of a pendulum using trigonometry and data from a table. The velocity and kinetic energy of the pendulum bob are also calculated and compared. The question of whether or not energy is conserved is raised, as well as the possibility of the pendulum eventually slowing down and stopping. The length of the string is represented by "L" in the equations, and the diameter is given as 2 cm. The motion of the pendulum can be approximated to simple harmonic motion, and experimental error must be taken into consideration when using the data from the table.
  • #1
aizeltine
20
0

Homework Statement

For the conservationofenergy,calculate the starting height of the bob. This is done with some trigonometry and is
∆h=L−Lcosθ
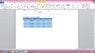
Calculate the initial potential energy of the pendulum for each of your starting angles.Now, using the diameter of the hanging mass (2 cm),and the time it took to pass through the photogate (***), calculate the velocity of the pendulum bob at the bottom of its swing.Using that velocity, calculate the kinetic energy of the pendulum bob.
•Compare the initial potential energy to the kinetic energy of the bob for each angle. Find the percent difference for each. Was energy conserved?
•If you let the pendulum continue to swing,it will eventually slow down and stop. Does this violate the conservation of energy?Why or whynot?

*** THE IMAGE OF THE DATA TABLE CAN BE SEEN AT :https://www.chegg.com/homework-help/questions-and-answers/pendulum-questions-l-calculate-initial-potential-energy-using-data-using-diameter-hanging--q7017035

I ATTACHED THIS IMAGE BELOW SO U DONT HAVE TO CLICK ANY LINK.

Homework Equations



∆h=L−Lcosθ, ... Diameter =2 cm

The Attempt at a Solution


Ok. Well, I am not really sure what L means in terms of my data..and the other questions i don't really know, I am a chem major and don't know anyhting about physics. I need help and guidance with the calculation questions. and the theoretical questions, i don't have any idea lol
 

Attachments

  • TAble ata.jpg
    TAble ata.jpg
    30.3 KB · Views: 424
Physics news on Phys.org
  • #2
##l## is the length of the string. Draw a diagram and you should be able to see why ##\delta h## is calculated using that expression. With the values given in the table, you should be able to compute the change in potential energy of the bob after it is released and reaches the bottom of the swing.

Does any equation come to your mind for calculating the velocity at the bottom? Remember that you have to take experimental error into consideration when using the values in the table.
Hint: This motion can be approximated to simple harmonic motion (the angle is small enough). Try integration.
 

FAQ: Solving Pendulum Questions: Calculate Initial PE & KE

How do I calculate the initial potential energy of a pendulum?

To calculate the initial potential energy of a pendulum, you will need to know the mass of the pendulum, the acceleration due to gravity, and the height of the pendulum at its starting position. The equation for calculating potential energy is PE = mgh, where m is the mass, g is the acceleration due to gravity, and h is the height.

How do I calculate the initial kinetic energy of a pendulum?

The initial kinetic energy of a pendulum can be calculated using the equation KE = 1/2mv^2, where m is the mass and v is the velocity of the pendulum at its starting position. To find the velocity, you can use the equation v = √(2gh), where h is the height of the pendulum at its starting position.

What is the relationship between potential energy and kinetic energy in a pendulum?

In a pendulum, potential energy is converted to kinetic energy and vice versa as the pendulum swings back and forth. At the highest point of the swing, the potential energy is maximum and the kinetic energy is zero. At the lowest point of the swing, the kinetic energy is maximum and the potential energy is zero.

How does the length of a pendulum affect its potential and kinetic energy?

The length of a pendulum does not affect its potential energy, but it does affect its kinetic energy. A longer pendulum will have a greater potential energy at its starting position, but the same amount of potential energy will be converted to kinetic energy. However, a longer pendulum will take longer to complete one swing, meaning the kinetic energy will be spread out over a longer period of time.

Can I use the equations for potential and kinetic energy to solve for the velocity of a pendulum at any point in its swing?

Yes, the equations for potential and kinetic energy can be used to solve for the velocity of a pendulum at any point in its swing. However, it is important to note that the equations assume ideal conditions and do not take into account factors such as air resistance. In real-world situations, the velocity of a pendulum may vary slightly due to these factors.

Similar threads

Differential Equation for a Pendulum
Replies
21
Views
2K
Is the line integral of tangential force in pendulum equal to the negative of change in potential energy?
Replies
3
Views
403
Elementary pendulum equation of motion
Replies
7
Views
1K
Pendulum Conservation of Energy
Replies
31
Views
3K
Using Momentum, KE and PE to solve this skier velocity problem
Replies
13
Views
2K
The mass of the pendulum bob was determined on an electronic scale and
Replies
34
Views
4K
Question on pendulum and cord tension
Replies
5
Views
2K
Speed of a pendulum at lowest point
Replies
2
Views
9K
Determining the Spring Constant for a Pendulum with a Spring-Loaded Launcher
Replies
3
Views
1K
Finding the distance of a peg so that a pendulum can circle around it
Replies
2
Views
312

Hot Threads

Recent Insights

Back
Top