Solving Question through Inertial Frame: Challenges & Workings

[Spector989]

Homework Statement

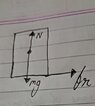
A rectangular plate is placed on a rough plank. Dimensions of the plank is as shown in the figure. Find:-
minimum acceleration with which the plank should be moved so that the rectangular plate topples (conside the friction is sufficient so the plate does not side).

Relevant Equations

Torque = r×F , friction = u.N , F= ma

So i solved this question through non inertial frame but how do i solve this through inertial frame , when i used to solve only translation question when i observed through non inertial frame the main difference was in inertial frame Fnet = 0 and in non inertial frame Fnet -ma =0 (ma being pseudo force ). But now the absecnce of ma (psuedo force ) in FBD leads to improper calculation of torque. How do i solve this through inertial frame . My workings in non interial frame and FBD for inertial frame are given in the picture attachment

 

[erobz]

PF prefers you use Latex to show your workings as opposed handwritten solutions. See the Latex Guide

 

[erobz]

When you solve the problem as you did, you are not using Newtons Laws in a non-inertial frame. We are applying a fictitious (inertial) force that converts the problem to an inertial frame. So, you DID solve it in an inertial frame.

 

[Spector989]

When you solve the problem as you did, you are not using Newtons Laws in a non-inertial frame. We are applying a fictitious (inertial) force that converts the problem to an inertial frame. So, you DID solve it in an inertial frame.

So the inertial force is Necessary?

 

[Spector989]

PF prefers you use Latex to show your workings as opposed handwritten solutions. See the Latex Guide

I am on my mobile and it will take me ages

 

[erobz]

So the inertial force is Necessary?

Using Newtons Laws, I believe so. What other method did you have in mind?

 

[Spector989]

Using Newtons Laws, I believe so. What other method did you have in mind?

Well the inertial force is fictious so i thought if i don't Include it in the fbd and observe from the ground i could have solved it somehow

 

[erobz]

Well the inertial force is fictious so i thought if i don't Include it in the fbd and observe from the ground i could have solved it somehow

You did observe it from the ground though. Those calculations are w.r.t. a frame of reference fixed to the ground?

 

[Spector989]

You did observe it from the ground though. Those calculations are w.r.t. a frame of reference fixed to the ground?

So why include the inertial force ?

 

[erobz]

So why include the inertial force ?

So...here is the problem (I think). Separate the block from the sled and do a FBD of the block. ( Ok never mind, I see you did that).

What is the force of static friction you calculated (I believe this is the point of confusion)?

 

[Spector989]

So...here is the problem (I think). Separate the block from the sled and do a FBD of the block. ( Ok never mind, I see you did that).

What is the force of static friction you calculated (I believe this is the point of confusion)?

 

[Spector989]

Force of friction = ma , m is the mass of the block accn is the, a is acceleration of platform as the block and platform are moving together

 

[erobz]

I get $a > \frac{g}{2}$ w.r.t a frame of reference fixed to the ground by summing the torques about the CM of the block.

 

[erobz]

In post #11:

The normal force is not applied to the CM. Where would the point of contact be when the box begins to tip?

 

[PeroK]

So i solved this question through non inertial frame but how do i solve this through inertial frame ,

It's conceptually more difficult in the inertial frame. Note first that torques must be considered about a fixed point in space; not about a point on an accelerating object (*).

As the block accelerates, the angular momentum about an origin (perhaps at the point where the rear of the block begins) is increasing. That requires a torque about that point, which must be provided by $mg$, as the accelerating force provides no torque about that point. If $a$ is large enough, then $mg$ is not sufficiently large to provide the required torque and the block starts to topple.

 

[Spector989]

It's conceptually more difficult in the inertial frame. Note first that torques must be considered about a fixed point in space; not about a point on an accelerating object (*).

As the block accelerates, the angular momentum about an origin (perhaps at the point where the rear of the block begins) is increasing. That requires a torque about that point, which must be provided by $mg$, as the accelerating force provides no torque about that point. If $a$ is large enough, then $mg$ is not sufficiently large to provide the required torque and the block starts to topple.

So the constraint is that mg must be able to handle the angular momentum?

 

[erobz]

It's conceptually more difficult in the inertial frame. Note first that torques must be considered about a fixed point in space; not about a point on an accelerating object (*).

As the block accelerates, the angular momentum about an origin (perhaps at the point where the rear of the block begins) is increasing. That requires a torque about that point, which must be provided by $mg$, as the accelerating force provides no torque about that point. If $a$ is large enough, then $mg$ is not sufficiently large to provide the required torque and the block starts to topple.

Is the shifting of $N$ to the corner of the box a manifestation of the inertial force?

 

[PeroK]

(*) PS consider an object falling under gravity. Now, there appears to be a torque about a point on the side of the object. Let's say it's a sphere, then this torque would be $mgR$, where $R$ is its radius. And the sphere ought to rotate. But, the same applies to the apparent torque on the opposite side. It ought to rotate in the opposite direction as well.

The answer is that you have to take the torque about a fixed point in space and in that case the increase in AM of the sphere about that point is provided simply by the sphere's linear acceleration (without rotation!) under gravity.

 

[PeroK]

Is the shifting of $N$ to the corner of the box a manifestation of the inertial force?

In the non-inertial frame, yes. Any normal force forward of the rear is only adding to the anticlockwise torque in this case. The first thing that happens is that the normal force increases towards the rear, up to a maximum of $mg$. That's what happens when you stand on an accelerating vehicle: the amount of weight on your back leg increases until that leg bears all your weight.

 

[PeroK]

So the constraint is that mg must be able to handle the angular momentum?

Provide the torque for the required increase in AM, yes. You should do the problem this way (in the inertial frame). It's more complex for sure.

Using the non-inertial frame was the simple way to solve the problem.

 

[Spector989]

Provide the torque for the required increase in AM, yes. You should do the problem this way (in the inertial frame). It's more complex for sure.

Using the non-inertial frame was the simple way to solve the problem.

Could you show me how to solve this using relation between angular momentum and torque , if it is complicated i can try and understand if not i can always stick to the easy method but the whole reason i made this thread was to better my concepts

 

[PeroK]

Could you show me how to solve this using relation between angular momentum and torque , if it is complicated i can try and understand if not i can always stick to the easy method but the whole reason i made this thread was to better my concepts

$$\vec \tau = \frac{d\vec L}{dt}$$Which, for planar problems can be simplified to$$\tau = \frac{dL}{dt}$$where for the x-y plane the AM and torque vectors are in the z-direction.

 

[PeroK]

An important point is that if we have a particle moving with constant velocity $v$ along the line $y = h$, then it has constant, non-zero angular momentum about the origin of $L = mvh$. And, if it is accelerating along that straight line, then the angular momentum is increasing:$$\frac{dL}{dt} = mah$$And the linear accelerating force represents a torque about the origin.

Some introductory texts imply that angular momentum applies to "rotational" motion, but this is wrong. Angular momentum applies to straight line motion - and indeed all motion.

 

[Spector989]

An important point is that if we have a particle moving with constant velocity $v$ along the line $y = h$, then it has constant, non-zero angular momentum about the origin of $L = mvh$. And, if it is accelerating along that straight line, then the angular momentum is increasing:$$\frac{dL}{dt} = mah$$And the linear accelerating force represents a torque about the origin.

Some introductory texts imply that angular momentum applies to "rotational" motion, but this is wrong. Angular momentum applies to straight line motion - and indeed all motion.

Yeah , i was confused too when we were taught that but when our teacher gave us some examples and plotted in on a graph made sense

 

[Spector989]

Thanks for the help , the topic makes more sense now :)