mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
I have to show that a set is recursive if and only if the set and its complement is recursively enumerable.
I have done the following:
$\Rightarrow$
Let $A$ the recursive set, so there is a Turing machine $M$ that decides the set $A$. We construct a TM $M'$ that semi-decides the set $A$. If the TM $M$ accepts the input, then the TM $M'$ accepts the input too. If the TM $M$ doesn't accept the input, then the TM $M'$ doesn't halt on this input.
That means that there is a TM that semi-decides te set $A$. So, any recursive set is recursively enumerable.
If the set $A$ is recursive there is a TM $M$ that decides the set $A$. We construct a TM $M''$ that decides the set $A^c$. If the TM $M$ accepts the input, then the TM $M''$ doesn't accept the input and if the TM $M$ doesn't accept the input, then the TM $M''$ accepts it.
So, if the set $A$ is recursive, the complement is also recursive. So, the set $A^c$ is also recursively enumerable. That means that if the set $A$ is recursive, then the sets $A$ and $A^c$ are recursively enumerable.
$\Leftarrow$
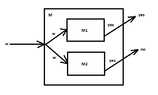
Let $A$ and $A^c$ be recursively enumerable. That means that there are TM $M_1$ and $M_2$ that semi-decides the set $A$ and $A^c$ respectively. We construct a TM $M$ that simulates simultaneously $M_1$ and $M_2$. $M$ accepts the input if $M_1$ accepts it and rejects it if $M_2$ accepts it. Since the input is either in $A$ or in $A^c$ exactly one of $M_1$ or $M_2$ will accept. That means that $M$ will always have the output either "yes" or "no", but will never have both.
That means that there is a TM that accepts $A$. So, $A$ is recursive. Is this correct? Could I improve something?
I have to show that a set is recursive if and only if the set and its complement is recursively enumerable.
I have done the following:
$\Rightarrow$
Let $A$ the recursive set, so there is a Turing machine $M$ that decides the set $A$. We construct a TM $M'$ that semi-decides the set $A$. If the TM $M$ accepts the input, then the TM $M'$ accepts the input too. If the TM $M$ doesn't accept the input, then the TM $M'$ doesn't halt on this input.
That means that there is a TM that semi-decides te set $A$. So, any recursive set is recursively enumerable.
If the set $A$ is recursive there is a TM $M$ that decides the set $A$. We construct a TM $M''$ that decides the set $A^c$. If the TM $M$ accepts the input, then the TM $M''$ doesn't accept the input and if the TM $M$ doesn't accept the input, then the TM $M''$ accepts it.
So, if the set $A$ is recursive, the complement is also recursive. So, the set $A^c$ is also recursively enumerable. That means that if the set $A$ is recursive, then the sets $A$ and $A^c$ are recursively enumerable.
$\Leftarrow$
Let $A$ and $A^c$ be recursively enumerable. That means that there are TM $M_1$ and $M_2$ that semi-decides the set $A$ and $A^c$ respectively. We construct a TM $M$ that simulates simultaneously $M_1$ and $M_2$. $M$ accepts the input if $M_1$ accepts it and rejects it if $M_2$ accepts it. Since the input is either in $A$ or in $A^c$ exactly one of $M_1$ or $M_2$ will accept. That means that $M$ will always have the output either "yes" or "no", but will never have both.
That means that there is a TM that accepts $A$. So, $A$ is recursive. Is this correct? Could I improve something?