Laplace Equation for an annular geometry with different BC

[stockzahn]

Dear all,

I would need mathematical help to solve for the temperature field in an annular geometry (you find a picture attached below the text):

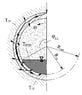
A copper pipe containing a boiling two-phase flow (in the stratified regime) is immersed in a liquid bath, which temperature $T_{IY}$ is assumed to be constant in the entire cross section. The heat transfer coefficient between the bath and the outer surface of the copper pipe($h_{out}$) is constant.

The liquid phase and the gas phase of the inside flow are in thermodynamic equilibrium ($T_{liq}=T_{gas}=T_{BHX}$). The heat transfer coefficient between the copper pipe and the gas $h_{Dry}$ is much lower than the heat transfer coefficient between the copper pipe and the liquid $h_{Wet}$.

The geometry is symmetric with respect to the vertical axis, the liquid level can be expressed as the angle $\varphi_{LL}$. $R_{in}$ and $R_{out}$ denote the inner and the outer radii of the copper pipe respectively.

2-dimensional Laplace equation for polar coordinates:

$$\frac{\partial^2 T}{\partial r^2}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^2}\frac{\partial^2 T}{\partial \varphi^2} = 0 \quad for\;R_{in}\leq r\leq R_{out},\;0\leq \varphi\leq 2\pi$$

With separation of the variables I obtained two correlations:

$$ g''\left(\varphi\right) + \lambda g\left(\varphi\right) =0$$
$$ r^2 f''\left(r\right) + r f'\left(r\right)-\lambda f\left(r\right) =0$$

Each linear combination of the solutions of the previous equations can be a solution, which generally reads

$$ T\left(r,\varphi\right)=c_0 + d_0 ln\left(r\right)+\sum\left(c_n r^{-n}+d_n r^{n}\right)\left(a_n cos\left(n\varphi\right)+b_n sin\left(n\varphi\right)\right) $$

Now, there are several boundary conditions for the first derivative in radial direction ($k$ denotes the (constant) heat conductivity of the copper):

$$\frac{\partial T}{\partial r}\bigg{|}_{r=R_{out}}=\frac{h_{out}}{k} \left(T_{IY}-T\right)\quad for\;0\leq\varphi\leq
\varphi_{LL}$$
$$\frac{\partial T}{\partial r}\bigg{|}_{r=R_{out}}=\frac{h_{out}}{k} \left(T_{IY}-T\right)\quad for\;\varphi_{LL}\leq\varphi\leq \pi$$
$$\frac{\partial T}{\partial r}\bigg{|}_{r=R_{in}}=\frac{h_{Dry}}{k}\ \left(T-T_{BHX}\right)\quad for\;0\leq\varphi\leq \varphi_{LL} $$
$$\frac{\partial T}{\partial r}\bigg{|}_{r=R_{in}}=\frac{h_{Wet}}{k} \left(T-T_{BHX}\right)\quad for\;\varphi_{LL}\leq\varphi\leq \pi $$

Due to the symmetry, also for the first derivative in tangential direction two boundary conditions can be found:

$$ \frac{\partial T}{\partial \varphi}\bigg{|}_{\varphi=0}=0 $$
$$ \frac{\partial T}{\partial \varphi}\bigg{|}_{\varphi=\pi}=0 $$

Finally, at the position $\varphi=\varphi_{LL}$, two transitional conditions can be set up:

$$T_{Dry}{\left(\varphi= \varphi_{LL}\right)}=T_{Wet}{\left(\varphi= \varphi_{LL}\right)}$$
$$ \frac{\partial T_{Dry}}{\partial \varphi}\bigg{|}_{\varphi=\varphi_{LL}}=\frac{\partial T_{Wet}}{\partial \varphi}\bigg{|}_{\varphi=\varphi_{LL}}$$

All together I have eight boundary conditions, but twelve unknown constants:

$$\underbrace{c_{0},d_{0},a_{n},b_{n},c_{n},d_{n}}_{\cdot 2\;for\;the\;wetted\;perimeter\;and\;the\;dry\;perimeter}$$

Unfortunately I'm not even sure, if this could be a way to solve the problem or if I made elementary mistakes. I hope that I used the mathematical symbols and notations correctly and gave any necessary information. Any help is appreciated.

Thanks in advance,
stockzahn

 

[Orodruin]

Your boundary conditions in the $\varphi$-direction should be $2\pi$ periodicity, which is already covered by the phase of the trigonometric functions being $n\pi\varphi$. However, you can further argue that half of the angular base functions (which?) can be disregarded as they do not satisfy the reflection symmetry of the problem.

You should definitely not use different constants for the pipe at different angles. What you are trying to do is an expansion in the base functions of the angular differential operator and it is therefore extremely important to use the entire range of $\varphi$ in the expansion. The idea of variable separation is based on having a Sturm-Liouville operator, in your case $-\partial_\varphi^2$, with appropriate boundary conditions, in your case $2\pi$ periodicity. You can then use Sturm-Liouville's theorem, which states that the eigenfunctions of the SL operator forms a basis for the appropriate $2\pi$ periodic functions of $\varphi$. In essence, for any fixed $r$ your target function (in this case the temperature in the pipe) can be written on the form
$$
T(r,\varphi) = \sum_n T_n(r) e^{in\varphi}.
$$
Note that I am using the complex form of the eigenfunctions here with $-\infty < n < \infty$, since it is easier to write it than to separately treat the $n = 0$ case. Inserted into the Laplace equation, this gives you the differential equation for $T_n(r)$ (after noting that all of the $e^{in\varphi}$ are linearly independent).

In order to obtain the appropriate boundary conditions for $T_n(r)$, you will now need to expand the inhomogeneities as well as the heat transfer coefficient in the boundary conditions in terms of the eigenfunctions $e^{in\varphi}$. Since the inner boundary condition depends on $\varphi$, this will mean that your differential equations for $T_n(r)$ generally do not decouple. However, you will get a (infinite) set of algebraic equations to solve.

All together I have eight boundary conditions, but twelve unknown constants:

This is not correct. You have an infinite number of constants, as in any problem where you expand in an infinite basis. Your boundary conditions, when expanded in terms of the eigenfunctions, will also give an infinite number of relations that should be sufficient to solve your problem.

 

[stockzahn]

Thanks for the fast response/help, I will try to process the information you gave me and maybe (probably / for sure) will have some more questions.

This is not correct. You have an infinite number of constants, as in any problem where you expand in an infinite basis. Your boundary conditions, when expanded in terms of the eigenfunctions, will also give an infinite number of relations that should be sufficient to solve your problem.

That, without a doubt, was a very stupid thought - thanks for the correction.

 

[stockzahn]

I'm pretty sure that I didn't understand everything you wrote. I try to explain, what I think:

You should definitely not use different constants for the pipe at different angles. What you are trying to do is an expansion in the base functions of the angular differential operator and it is therefore extremely important to use the entire range of $\varphi$ in the expansion. The idea of variable separation is based on having a Sturm-Liouville operator, in your case $-\partial_\varphi^2$, with appropriate boundary conditions, in your case $2\pi$ periodicity. You can then use Sturm-Liouville's theorem, which states that the eigenfunctions of the SL operator forms a basis for the appropriate $2\pi$ periodic functions of $\varphi$.

So my two equations are the Sturm-Liouville Eigenvalue problem (1) and the Euler Differential Equation (2).

$$ g''\left(\varphi\right) + \lambda g\left(\varphi\right) =0 \qquad \text{(1)}$$
$$ r^2 f''\left(r\right) + r f'\left(r\right)-\lambda f\left(r\right) =0 \qquad \text{(2)}$$

The solution for (1): $g_0\left(\varphi\right) = a_0$ and $g_n\left(\varphi\right) = a_n cos\left(n\varphi\right)+b_n sin\left(n\varphi\right)$ (expressed as $e^{in\varphi}$)
The solution for (2): $f_0\left(r\right) =c_0+d_0 ln\left(r\right)$ and $f_n\left(r\right) =c_n r^{-n}+d_n r^{n}$ (expressed as $T_n(r)$)

Therefore you expressed the solution
$$ T\left(r,\varphi\right)= f\left(r\right) g\left(\varphi\right) $$
as
$$T(r,\varphi) = \sum_n T_n(r) e^{in\varphi}.$$

In essence, for any fixed $r$ your target function (in this case the temperature in the pipe) can be written on the form

$$

T(r,\varphi) = \sum_n T_n(r) e^{in\varphi}.

$$

Note that I am using the complex form of the eigenfunctions here with $-\infty < n < \infty$, since it is easier to write it than to separately treat the $n = 0$ case. Inserted into the Laplace equation, this gives you the differential equation for $T_n(r)$ (after noting that all of the $e^{in\varphi}$ are linearly independent).

Now inserting it into the Laplace equation yields

$$ \Delta T\left(r,\varphi\right)=\sum \left[T_n''\left(r\right)+\frac{1}{r}T_n'\left(r\right)-\frac{n^2}{r^2}T_n\left(r\right)\right]e^{in\varphi} = 0$$
$$ \sum \left[T_n''\left(r\right)+\frac{1}{r}T_n'\left(r\right)-\frac{n^2}{r^2}T_n\left(r\right)\right] = 0$$

In order to obtain the appropriate boundary conditions for $T_n(r)$, you will now need to expand the inhomogeneities as well as the heat transfer coefficient in the boundary conditions in terms of the eigenfunctions $e^{in\varphi}$. Since the inner boundary condition depends on $\varphi$, this will mean that your differential equations for $T_n(r)$ generally do not decouple. However, you will get a (infinite) set of algebraic equations to solve.

To expand the BCs in terms of $e^{in\varphi}$, I need to create a Fourier series like

$$ \frac{\partial T}{\partial r}\left(\varphi\right)= \frac{a_0}{2} + \sum\limits_{n=1}^\infty \left[ a_n cos\left(n\varphi\right) +b_n sin\left(n\varphi\right) \right],$$

which describes "the shape" of my boundary conditions along the angle $\varphi$ at $R_{in}$ and $R_{out}$. However, in my case the BC includes the temperature, which I want to calculate. So how can I expand a series to find the shape of the BC, which is obtained by the result?

$$\frac{\partial T}{\partial r}\bigg{|}_{R_{out},\varphi}=\frac{h_{out}}{k} \left(T_{IY}-T\left(R_{out},\varphi\right)\right)= \frac{a_0}{2} + \sum\limits_{n=1}^\infty \left[ a_n cos\left(n\varphi\right) +b_n sin\left(n\varphi\right) \right]$$

$$\frac{\partial T}{\partial r}\bigg{|}_{R_{in},\varphi}=\frac{h_{in}}{k} \left(T\left(R_{in},\varphi\right)-T_{BHX}\right)= \frac{a_0}{2} + \sum\limits_{n=1}^\infty \left[ a_n cos\left(n\varphi\right) +b_n sin\left(n\varphi\right) \right]$$

Your boundary conditions in the $\varphi$-direction should be $2\pi$ periodicity, which is already covered by the phase of the trigonometric functions being $n\pi\varphi$. However, you can further argue that half of the angular base functions (which?) can be disregarded as they do not satisfy the reflection symmetry of the problem.

The cosine is the even function, the sine is the odd function. Since the geometry is axisymmetrical with respect to the vertical axis, I'd say the cosine function reflects the symmetry of my problem.

Thanks again for the support!

 

[Orodruin]

Therefore you expressed the solution
$$ T\left(r,\varphi\right)= f\left(r\right) g\left(\varphi\right) $$
as
$$T(r,\varphi) = \sum_n T_n(r) e^{in\varphi}.$$

Your first expression here is not the general solution. What I did was to fix $r$ and expand the solution in the $\varphi$ eigenfunctions of the SL operator. Since the function being expanded depends on $r$, so do the expansion coefficients $T_n$.

Now inserting it into the Laplace equation yields

$$ \Delta T\left(r,\varphi\right)=\sum \left[T_n''\left(r\right)+\frac{1}{r}T_n'\left(r\right)-\frac{n^2}{r^2}T_n\left(r\right)\right]e^{in\varphi} = 0$$
$$ \sum \left[T_n''\left(r\right)+\frac{1}{r}T_n'\left(r\right)-\frac{n^2}{r^2}T_n\left(r\right)\right] = 0$$

Your last step here is not valid. You cannot just throw away the $\varphi$ basis functions. The point is that those basis functions are all linearly independent and to make the entire sum zero, the prefactor must be equal to zero for each term, leading to a homogeneous differential equation for $T_n(r)$. Up to this point you really had no handle on what differential equation those prefactors should satisfy. (This is the reason separation of variables works although it usually is not presented this way!)

To expand the BCs in terms of $e^{in\varphi}$, I need to create a Fourier series like

$$ \frac{\partial T}{\partial r}\left(\varphi\right)= \frac{a_0}{2} + \sum\limits_{n=1}^\infty \left[ a_n cos\left(n\varphi\right) +b_n sin\left(n\varphi\right) \right],$$

which describes "the shape" of my boundary conditions along the angle $\varphi$ at $R_{in}$ and $R_{out}$. However, in my case the BC includes the temperature, which I want to calculate. So how can I expand a series to find the shape of the BC, which is obtained by the result?

$$\frac{\partial T}{\partial r}\bigg{|}_{R_{out},\varphi}=\frac{h_{out}}{k} \left(T_{IY}-T\left(R_{out},\varphi\right)\right)= \frac{a_0}{2} + \sum\limits_{n=1}^\infty \left[ a_n cos\left(n\varphi\right) +b_n sin\left(n\varphi\right) \right]$$

$$\frac{\partial T}{\partial r}\bigg{|}_{R_{in},\varphi}=\frac{h_{in}}{k} \left(T\left(R_{in},\varphi\right)-T_{BHX}\right)= \frac{a_0}{2} + \sum\limits_{n=1}^\infty \left[ a_n cos\left(n\varphi\right) +b_n sin\left(n\varphi\right) \right]$$

You already have an expansion for $T$ and so you can express both $T$ and $T_r$ at the boundaries in terms of those. What you need to do is to also expand the heat transfer coefficients in the basis functions. This will give you some relations that should essentially fix your constants. I also suggest you make a translation so that the inner temperature is zero. This will remove some complications from your boundary conditions.

The cosine is the even function, the sine is the odd function. Since the geometry is axisymmetrical with respect to the vertical axis, I'd say the cosine function reflects the symmetry of my problem.

This is correct. You can just throw away the sines because of the symmetry.

 

[stockzahn]

Your first expression here is not the general solution. What I did was to fix $r$ and expand the solution in the $\varphi$ eigenfunctions of the SL operator. Since the function being expanded depends on $r$, so do the expansion coefficients $T_n$.

Your last step here is not valid. You cannot just throw away the $\varphi$ basis functions. The point is that those basis functions are all linearly independent and to make the entire sum zero, the prefactor must be equal to zero for each term, leading to a homogeneous differential equation for $T_n(r)$. Up to this point you really had no handle on what differential equation those prefactors should satisfy. (This is the reason separation of variables works although it usually is not presented this way!)

The prefactor of $e^{in\varphi}$ equals zero results in the Euler Differential equation.

$$\Delta T\left(r,\varphi\right)=\sum \underbrace{\left[T_n''\left(r\right)+\frac{1}{r}T_n'\left(r\right)-\frac{n^2}{r^2}T_n\left(r\right)\right]}_{= 0}e^{in\varphi}$$
$$T_n''\left(r\right)+\frac{1}{r}T_n'\left(r\right)-\frac{n^2}{r^2}T_n\left(r\right)=0 \rightarrow \text{Euler DE}$$

The solution of the Euler DE is

$$T_n\left(r\right)=c_nr^{-n}+d_nr^{n}$$

Now I have the coefficients $c_n$ and $d_n$ for each $n$, for which I need the BC to calculate them.

$$T\left(r,\varphi\right)=\sum \left(c_nr^{-n}+d_nr^{n}\right) e^{in\varphi}$$

I hope the problem was the argumentation/way of the derivation, because I've already had something similar. Otherwise I didn't understand the problem.

This is correct. You can just throw away the sines because of the symmetry.

Euler's formula says

$$e^{in\varphi}= cos\left(n\varphi\right)+i\,sin\left(n\varphi\right),$$

since I can neglect the sine-terms it can be simplified to

$$e^{in\varphi}= cos\left(n\varphi\right).$$

Using that correlation, the entire formula can be written:

$$T\left(r,\varphi\right)=\sum \left(c_nr^{-n}+d_nr^{n}\right) cos\left(n\varphi\right)$$

For the $2n$ coefficients, I now have to find the expansions of the heat transfer coefficients.

You already have an expansion for $T$ and so you can express both $T$ and $T_r$ at the boundaries in terms of those. What you need to do is to also expand the heat transfer coefficients in the basis functions. This will give you some relations that should essentially fix your constants.

$$T=\sum \left(c_nr^{-n}+d_nr^{n}\right) cos\left(n\varphi\right)$$
$$T_r=\sum \left(-nc_nr^{-\left(n+1\right)}+nd_nr^{n-1}\right) cos\left(n\varphi\right)$$

Since the heat transfer coefficient at the outer surface and the thermal conductivity are constant, I suppose I don't need an expansion for the outside BC.

$$T_r\big{|}_{r=R_{out}}=\frac{h_{out}}{k} \left(T_{IY}-T\big{|}_{r=R_{out}}\right)$$
$$\sum \left(-nc_nR_{out}^{-\left(n+1\right)}+nd_nR_{out}^{n-1}\right) cos\left(n\varphi\right)=\frac{h_{out}}{k} \left(T_{IY}-\sum \left(c_nR_{out}^{-n}+d_nR_{out}^{n}\right) cos\left(n\varphi\right)\right)$$

At the inner surface though, the heat transfer coefficient does vary. Therefore I need an expansion to create the right shape. I tried to find one like

$$h_{in}\left(\varphi\right)=h_{Wet}-\frac{\left(h_{Wet}-h_{Dry}\right)}{\pi}\left[\varphi_{LL}+2\sum\limits_{n=1}^{\infty}\frac{sin\left(n\varphi_{LL}\right)}{n}cos\left(n\varphi\right)\right],$$

whose curve you can find in the diagram attached at the end of the post. This correlation I can insert into the BC:

$$T_r\big{|}_{r=R_{in}}=\frac{h_{in}\left(\varphi\right)}{k} \left(T\big{|}_{r=R_{in}}-T_{BHX}\right)$$
$$\sum \left(-nc_nR_{in}^{-\left(n+1\right)}+nd_nR_{in}^{n-1}\right) cos\left(n\varphi\right)=\frac{h_{in}\left(\varphi\right)}{k} \left[\sum \left(c_nR_{out}^{-n}+d_nR_{out}^{n}\right)cos\left(n\varphi\right)-T_{BHX}\right] $$

I also suggest you make a translation so that the inner temperature is zero. This will remove some complications from your boundary conditions.

I suppose with inner temperature you meant $T_{BHX}$, therefore

$$\sum \left(-nc_nR_{in}^{-\left(n+1\right)}+nd_nR_{in}^{n-1}\right) cos\left(n\varphi\right)=\frac{h_{in}\left(\varphi\right)}{k} \left[\sum \left(c_nR_{out}^{-n}+d_nR_{out}^{n}\right)cos\left(n\varphi\right)\right]$$

$$\sum \left(-nc_nR_{out}^{-\left(n+1\right)}+nd_nR_{out}^{n-1}\right) cos\left(n\varphi\right)=\frac{h_{out}}{k} \left(\underbrace{T_{IY}-T_{BHX}}_{T_{0}}-\sum \left(c_nR_{out}^{-n}+d_nR_{out}^{n}\right) cos\left(n\varphi\right)\right)$$

Would that be the correct approach to be able solve the problem?

 

[stockzahn]

Just an update: I tried to solve the problem with my approach and I've got the first results. After my post you find diagrams with the temperature profiles for $0\leq\varphi\leq\pi$ with $\varphi_{LL}=\pi/2$. Some comments:

1) The calculations of the sums only was possible for $-110\leq n\leq 226$, since all other values for $n$ yield numbers to high or to low for the programm to process.

2) At the value $n=0$ yields a division by zero. Therefore I didn't take this value into account when calculating the sums.

3) Using the actual parameters of the problem, the resulting curves look strange and the obtained values for the temperatures are wrong ($T_{max}=1.9\;K$). This can be seen in the first three diagrams, which illustrate the temperature profile at three different radii (inner surface $R_{in}$, half wall thickness $R_{BHX}$ and outer surface $R_{out}$). By increasing the heat conductivity of the copper by a factor of 100, the resulting profiles become realistic (as illustrated in the last diagram).

Thanks for your help until now. If you have any other hint or correction, I would be grateful.

 

[Orodruin]

2) At the value $n=0$ yields a division by zero. Therefore I didn't take this value into account when calculating the sums.

Typically the $n = 0$ term is very important. However, you cannot treat it along with the others as $\cos(nx)$ for $n = 0$ does not integrate to $\sin(nx)/n$, it integrates to $x$.