Some questions about Noise and Power spectral Density

[baby_1]

Hello
I've got confused about some features of noise.
1)Can use noise a generator?

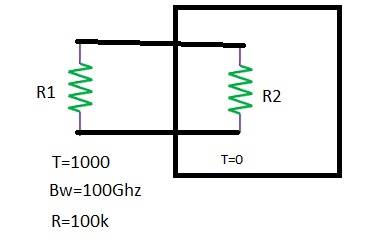
Well , if we have a noisy resistor and Ideal resistor why can't we use noise voltage according to noise voltage $$Vn=\sqrt(4KTBR)$$

2)why we divide power spectral density to RL( load) when we find power at RL?(it is a normalized voltage^2)?
3)for shot noise, it is better to decrease or increase DC current to reduce noise effect?because according to shot noise current $I_{s}=\sqrt{2I_{dc}qBw}$ I understand we should reduce DC current to decrease noise current but in book text it has mentioned that we should reduce DC current to decrease noise voltage, which is correct and why?

Thanks in advance

 

[Paul Colby]

In your diagram there is heat flow from R1 into R2. (I'm also confused by noise)

 

[baby_1]

Thanks Paul for your comment.
I have been confused so far

 

[Paul Colby]

Part of the issue is I don't understand your question as worded. A noisy resistor is an ideal resistor with a series ideal voltage generator (i.e. the noise). The noisy resistor is (I assume) $R1$ since it is at $T=1000K$. The noise voltage will appear divided across $R1$ and $R2$ where $v1 = \frac{R1}{R1+R2}V_n$ and $v2=\frac{R2}{R1+R2}V_n$. Does this help?

 

[baby_1]

Thanks Paul Colby for your explanation
Sorry if I explained my problem badly , As a matter of fact as you see we have a noise voltage across the R2 resistor that comes from R1 noise , So I want to know why we can't use this voltage to bias R2? for example if we change R2 with a transistor why It can't bias the transistor? (if we select a high resistor value or high bandwidth ?)

Thanks in advance

 

[Paul Colby]

Well, in principle one could rectify the broadband noise at $R2$ supplied by $R1$ and extract energy. This is only possible because $R2$ is at a lower temperature than $R1$. As I said, in this case there is heat flow. In this case power could be extracted. BTW this would be no different than running a photocell from the light of a fire. Only the transmission is through space rather than through a wire.

On the flip side. If the temperatures are the same, then the power flow is the same in both directions and no net power may be extracted.