Period and Velocity of Oscillating Sphere Attached to Spring

[Nexus99]

Homework Statement

Work in progress

Relevant Equations

Pure rolling condition

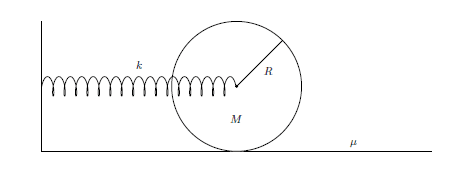
A homogeneous sphere of mass M and radius R is at rest on a rough horizontal plane with coefficient
of static friction μ . A spring of elastic constant k, is connected to the rotation axis of the sphere
illustrated in the figure. The center of mass of the sphere is positioned at rest so that the spring is
lengthened by a stretch equal to L, determine:
a) the period of oscillations of the sphere;
b) the maximum angular velocity of the sphere;
c) the maximum value of L for which the pure rolling speed is maintained.

I tried in this way:
a) if there is an oscillation there is no static friction but dynamic:
Projecting the two cardinal equations along the axis and considering the center of mass of the sphere the point about which the torque is being measured:

-F_{r} - kL = ma
F_{r}R = Ialpha = I a/R = 2/5MRa

F_{r} = 2/5Ma
- 5/7kL = ma k' = 5/7k
-k'L = ma

that is the equation of an harmonic oscillator with ω = √(5/7 k m), that represent the period of oscillations of the sphere, is this solution right?

 

[haruspex]

if there is an oscillation there is no static friction but dynamic:

That's a strange statement.. did you mean that?
Your equations assume static friction (αR=a).

 

[Nexus99]

Yes, i realized after that i was wrong but i forgot to delete it
as for the procedure, is it correct?

 

[haruspex]

Yes, i realized after that i was wrong but i forgot to delete it
as for the procedure, is it correct?

This is not quite right:

√(5/7 k m)

It is dimensionally wrong. You left out something. Other than that, I think it is ok.

 

[Nexus99]

This is not quite right:

It is dimensionally wrong. You left out something. Other than that, I think it is ok.

Yes, i forgot a /, it should be:
ω = √(5/7 k/m)
thanks for help

 

[Delta2]

Very nice problem ( I like it a a lot really thanks for posting it @Okpluto )
For b) you got to be carefull not to confuse the angular velocity (or angular frequency) of oscillation with the angular velocity of the sphere
for c) you have already derived that for pure rolling we have $$F_r=\frac{2}{5}Ma$$. This becomes max when the acceleration $a$ becomes max and equal to $\omega^2L$. We have to impose that $$max( F_r)\leq max(static friction)$$.

 

[etotheipi]

Alternative method of solution: conserve energy. Let $$E = \frac{1}{2}m\dot{x}^2 + \frac{1}{2}I\omega^2 + \frac{1}{2}kx^2 = \frac{1}{2}m\dot{x}^2 + \frac{1}{2}\times \frac{2}{5}mr^2 \times {\left(\frac{\dot{x}}{r}\right)}^2 + \frac{1}{2}kx^2$$ and then set $\frac{dE}{dt} = 0$ since friction does no work during rolling: $$\frac{dE}{dt} = \frac{7}{5}m\dot{x}\ddot{x} + kx\dot{x} = 0 \implies \ddot{x} = -\frac{5k}{7m}x$$

 

[wrobel]

I think one should first assume that the system moves without slipping and find the friction force $F=F(x,h)$ where $x$ is the coordinate of the center of disk and $h$ is a constant of the energy integral. Then to consider the condition $|F(x,h)|\le \mu mg$

 

[Nexus99]

Very nice problem ( I like it a a lot really thanks for posting it @Okpluto )
For b) you got to be carefull not to confuse the angular velocity (or angular frequency) of oscillation with the angular velocity of the sphere
for c) you have already derived that for pure rolling we have $$F_r=\frac{2}{5}Ma$$. This becomes max when the acceleration $a$ becomes max and equal to $\omega^2L$. We have to impose that $$max( F_r)\leq max(static friction)$$.

I solved b and c in this way:

EDIT: $$v_{cm} = \Omega R$$ not small omega
I had to write it in a Latex compiler because for me, in this forum, Latex doesn't always work for

 

[Delta2]

I solved b and c in this way:

View attachment 263776

EDIT: $$v_{cm} = \Omega R$$ not small omega
I had to write it in a Latex compiler because for me, in this forum, Latex doesn't work (as you can see)

I think you are correct for b) and c). You could also do b) by using the equation of harmonic oscillator $x=L\sin\omega t$ and $v_{CM}=\dot{x}=\omega L\cos\omega t$ and hence setting the max value of $$max( v_{CM})=\omega L=\Omega_{max} R $$

 

[Delta2]

There seem to be some problems with the rendering of Latex commands, I hope they are going to be fixed soon.