Spherical Geometry (Two dimension ) Defining a metric

[Arman777]

I am trying to understand how to define a metric for a positively curved two-dimensional space.I am reading a book and in there it says,

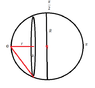
On the surface of a sphere, we can set up a polar coordinate system by picking a pair of antipodal points to be the “north pole” and “south pole” and by picking a geodesic from the north to south pole to be the “prime meridian”. If $r$ is the distance from the north pole, and $θ$ is the azimuthal angle measured relative to the prime meridian, then the distance ds between a point $(r,θ)$ and another nearby point $(r+dr,θ+dθ)$ is given by the relation
$$ds^2 = dr^2 + R^2sin^2(\frac {r}{R})dθ^2$$
where $R$ is the readius of the sphere.

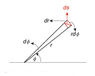
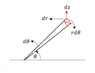
If I think ,flat two dimensional space the metric will be;
$$ds^2 = dr^2 + r^2dθ^2$$

I know the derivation of this so it gives me a bit clue about it,
In this case

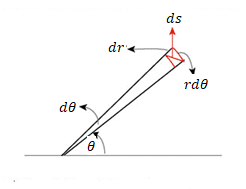
So in positively curved space instead of $rdθ$ we will have $R^2sin^2(\frac {r}{R})dθ$ which its kind of obvious.

So anyone who can help to understand the concept maybe an image ?

 

[Orodruin]

I am not sure I understand what your question is.

 

[Arman777]

I am not sure I understand what your question is.

I didnt understand where the $$ds^2 = dr^2 + R^2sin^2(\frac {r}{R})dθ^2$$ comes from. Like It writes there yes but I can't make a picture in my head...In example why there is sin function ?

 

[Orodruin]

Consider a circle on the sphere around one of the poles of radius $r$. What would be the circumference of this circle?

 

[Arman777]

So I guess I find it, here $k=Rsin(\frac {r}{R})$ cause when we set $r=R$ we should get a $k=R$.

So $$ds^2 = dr^2 + R^2sin^2(\frac {r}{R})dθ^2$$

In here its actually $ds^2 = dr^2 + k^2dθ^2$ ?

 

[Orodruin]

When you set $r = R$ you have an angle from the pole that corresponds to one radian and so you get $R \sin(1~\mbox{rad})$ as your $k$. Note that the $r$ you have marked in the figure is not the $r$ coordinate or the radius of the circle along the sphere's surface. The $r$ coordinate is the distance from the pole along the surface of the sphere.

 

[Arman777]

I need an image I guess..I am unfamilier with polar coordinates.Its hars for me to describe and understand in those terms.

 

[Arman777]

Consider a circle on the sphere around one of the poles of radius $r$. What would be the circumference of this circle?

$sin(r)$ ? where $0≤0≤π$ ?

 

[Arman777]

Consider a circle on the sphere around one of the poles of radius $r$. What would be the circumference of this circle?

$sin(r)$ ? where $0≤0≤π$ ?

 

[Arman777]

Is this metric can be also described as;

$ds^2=dr^2+sin^2(r)dθ^2$ ?

 

[Orodruin]

I need an image I guess..I am unfamilier with polar coordinates.Its hars for me to describe and understand in those terms.

Polar coordinates on the sphere work just as polar coordinates in a plane. You refer to a point by using the distance $r$ and direction $\theta$ from the origin.

 

[Arman777]

I guess I understand, For a case where unit circle $ds^2=dr^2+sin^2(r)dθ^2$ this is true. If we take a part of a circle in this sphere then the radius of the sphere will be $sin(r)$. But since its not a unit circle, the radius of a given circle in the sphere will be, $Rsin(\frac {r} {R})$ so then It turns just a normal circle metric.