knockout_artist
- 70
- 2
Hi,
I working on their text this equation did not make sense to me.
From equation 1 it differentiate second term , I wonder how he got second term of equation 2.
What I think is, what I wrote at the bottom
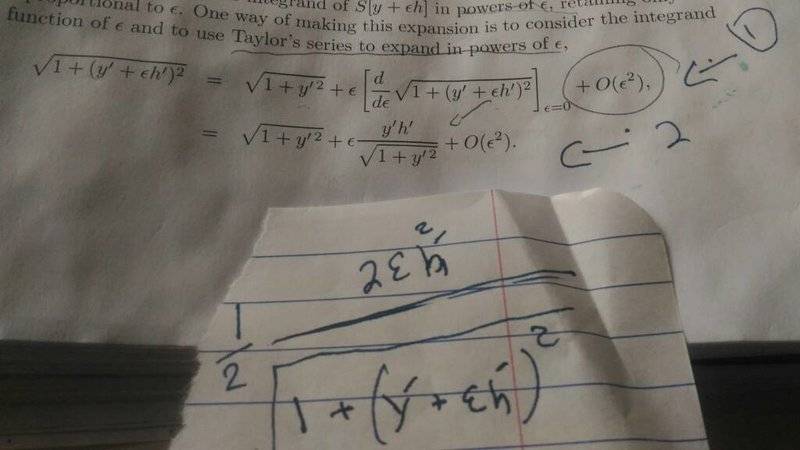
I working on their text this equation did not make sense to me.
From equation 1 it differentiate second term , I wonder how he got second term of equation 2.
What I think is, what I wrote at the bottom
