Static Equilibrium Problem Dealing with Torque

[PeachBanana]

Homework Statement

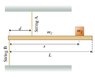
The figure shows a model of a crane that may be mounted on a truck. A rigid uniform horizontal bar of mass = 90.00 kg and length = 5.200 m is supported by two vertical massless strings. String A is attached at a distance = 1.600 m from the left end of the bar and is connected to the top plate. String B is attached to the left end of the bar and is connected to the floor. An object of mass = 3000 kg is supported by the crane at a distance = 5.000 kg from the left end of the bar.

Throughout this problem, positive torque is counterclockwise and use 9.807 m/s^2 for the magnitude of the acceleration due to gravity.


Find the tension in string A.

Homework Equations

This problem let's you use hints and it suggested I use the following equation with having the Tension in String "B" as the origin.

The Attempt at a Solution

Tension A(1.6000m) - (90.00 kg)(9.807 m/s^2) 1/2(5.200 m) - (3000 kg)(9.807 m/s^2)(5.000 m) = 0

I don't understand the "1/2" part in front of the length mass one. Is that because of where it is placed or its moment of inertia?

 

[PhanthomJay]

If the weight of the 90 kg beam is uniformly distributed over its length, where does its resultant load act?

 

[PeachBanana]

I'm sorry, I'm not sure what you mean by resultant load.

 

[PhanthomJay]

I'm sorry, I'm not sure what you mean by resultant load.

If a uniform beam that is 2 m long has a mass of 0.5 kg/m, its total mass is 1 kg and it's resultant or total weight is 9.8 N. It can be represented as a single force of 9.8 N acting at its center of gravity.