Discussion Overview
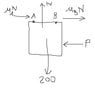
The discussion revolves around a statics problem involving a 200-LB door suspended from two rollers, A and B, with given coefficients of friction. Participants explore how to calculate the force required to move the door to the left, considering the effects of friction and the distribution of forces at the rollers.
Discussion Character
- Homework-related
- Mathematical reasoning
- Technical explanation
Main Points Raised
- One participant states that the normal force at each roller is 100 LB, assuming symmetry, but acknowledges uncertainty in their calculations.
- Another participant suggests that the pull force creates a moment about roller B, indicating that the downward force at roller A will be greater than 100 LB.
- A later reply outlines the equations needed to solve the problem, noting that the assumption of equal normal forces at A and B is incorrect.
- The participant who initially struggled expresses gratitude for the guidance received, indicating that they have arrived at a solution consistent with the book's answer.
- Final values presented include NA = 45.5 and NB = 154.5, leading to a calculated force P of 45.5 LB.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the initial assumptions regarding the normal forces at the rollers, as one participant corrects the assumption of symmetry. The discussion reflects a progression from confusion to clarity, but initial disagreements on the approach remain evident.
Contextual Notes
Participants note the importance of considering moments and the distribution of forces, highlighting that assumptions about equal normal forces can lead to errors in calculations. The discussion includes multiple equations and variables that are interconnected, which may complicate the resolution of the problem.

 Ok, in my defense, I am still a student and still learning.
Ok, in my defense, I am still a student and still learning.