Statics - Max Tension in Cables

[keximaze]

Please help

PROBLEM

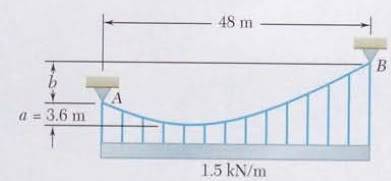
Cable AB supports a load distributed uniformly along the horizontal as shown. The lowest portion of the cable is located at a distance a = 3.6m below support A, and support B is located a distance b = na above A.

-> Determine the maximum tension in the cable as a function of n.

Homework Equations

The equation of the parabola the cable creates when an xy axes is placed at the lowest point of the cable, is
y = w(x^2) / 2*To

Key idea: the maximum tension is located at the support where the slope is maximum.

The Attempt at a Solution

I think I have to find the length xa first, then use the formula ya= w(xa)^2/ 2*To to get the formula for the tension. The problem is, I don't know how I could get xa.

Please help. Thanks

 

[tiny-tim]

hi keximaze!

(try using the X² and X₂ icons just above the Reply box )

I think I have to find the length xa first, then use the formula ya= w(xa)^2/ 2*To to get the formula for the tension. The problem is, I don't know how I could get xa.

(don't you mean x_b ? )

let the parabola be y = kx²

then you know kx_a² and kx_b², and you know x_a + x_b = 48

 

[keximaze]

hi keximaze!

(try using the X² and X₂ icons just above the Reply box )(don't you mean x_b ? )

let the parabola be y = kx²

then you know kx_a² and kx_b², and you know x_a + x_b = 48

Hello.
Yep, I meant x_b

I know that I have to exploit the relations between x_a, x_b, y_a, and y_b...But I don't know what you mean by "you know kx_a² and kx_b²"

Thanks.

 

[pongo38]

You know that the bending moment is zero at any point in the cable. By creful choice of two locations, you can use this to get two simultaneous equations for xB and yB. Admittedly the equations are non-linear, but they are solvable.

 

[keximaze]

You know that the bending moment is zero at any point in the cable. By creful choice of two locations, you can use this to get two simultaneous equations for xB and yB. Admittedly the equations are non-linear, but they are solvable.

Thanks for the hint...But I do not understand how to get these two equations

 

[pongo38]

Do you know how to write down an equilibrium equation, taking moments about a point? If you do, then ascribe arbitrary directions to the reaction components at B. Then take moments about A for the whole structure. The sum of the moments should be zero. Can you do that?

 

[tiny-tim]

hello keximaze!

...But I don't know what you mean by "you know kx_a² and kx_b²"

the question tells you that it is a parabola, so you know that (using the lowest point as the origin) the equation must be y = kx², and all you need to do is find k …

the question also gives you the height of A and B above the origin

 

[keximaze]

Do you know how to write down an equilibrium equation, taking moments about a point? If you do, then ascribe arbitrary directions to the reaction components at B. Then take moments about A for the whole structure. The sum of the moments should be zero. Can you do that?

That's what I did. I cut the cable where the lowest point is located, took the moment about a, and got
y_a = w_ax_a² / 2To for the left side and
y_b = w_bx_b² / 2To for the right side

and when I took the moment about A for the entire body, I obtained another equation.

hello keximaze!


the question tells you that it is a parabola, so you know that (using the lowest point as the origin) the equation must be y = kx², and all you need to do is find k …

the question also gives you the height of A and B above the origin

k = wb / (2*To) .....what does it mean?

 

[nvn]

keximaze: You are doing well, so far. Your first two equations, at the beginning of post 8, are correct. As you know, y_a = a, y_b = a + b = a + n*a = a*(n + 1), and w_a = w_b = w.

Your third equation is the very last equation in post 2.

You now have three equations. Solve them simultaneously for the unknowns (as a function of n, which is a known).