Stokes' Theorem for a Circle in a Plane

[flyusx]

Homework Statement

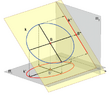
Find $\int_C \textbf{F}\cdot\text{d}\textbf{r}$ where $C$ is the circle of radius 1 in the plane $x+y+z=5$ centred at $(1,4,0)$ with a clockwise orientation when viewed from the origin and $\textbf{F}=\langle3y,3x,4(y-x)\rangle$

Relevant Equations

$\int_C\textbf{F}\cdot\text{d}\textbf{r}=\int_S(\nabla\times\textbf{F})\cdot\text{d}^{2}\textbf{r}$

I identified this as a Stokes theorem problem. I first took the curl of the vector field and got $\langle4,4,-6\rangle$. The surface integral becomes $$\int_S\langle4,4,-6\rangle\cdot\text{d}^{2}\textbf{r}$$

Here, I define $\text{d}^{2}\textbf{r}$ to be the differential area for an arbitrary coordinate system ($\text{d}x\text{d}y$, $r\text{d}r\text{d}\theta$, etc).

I can re-write this surface integral by parameterising the surface using $\textbf{r}(x,y)=\langle x,y,5-x-y\rangle$ and taking the cross product between the two partial derivatives of this parameterisation. The partial derivatives are $\langle1,0,-1\rangle$ and $\langle0,1,-1\rangle$, so the resultant cross product is $\langle1,1,1\rangle$. The clockwise orientation is negative so I use $\langle-1,-1,-1\rangle$. To evaluate the surface integral: $$\int_S\textbf{F}\cdot\text{d}^{2}\textbf{r}=\int_A\textbf{F}\cdot\left\vert\frac{\partial\textbf{r}}{\partial x}\times\frac{\partial\textbf{r}}{\partial y}\right\vert\text{d}^{2}\textbf{r}$$ where $A$ represents the $xy$ region yielding the parameterisation of the surface. The dot product returns 2 so the surface integral becomes $$2\int_A\text{d}^{2}\textbf{r}$$ I see $A$ to be the area of the circle with radius 1 (a total area of $\pi$) so the answer should be $2\pi$.



I found this to be incorrect (and $-2\pi$ is also incorrect). Perhaps my 'area' step is incorrect since I was specifically given where it was centered?

 

[Orodruin]

Your area is not $\pi$ as it should be the area in the $x$-$y$ coordinate plane. Your underlying problem is that what you call $\text{d}^{2}\textbf{r}$, the vector area element, is $\langle -1, -1, -1\rangle dx\, dy$, but the area covered in the $x$-$y$ plane by the relevant coordinate region is not $\pi$. The relevant curve is a circle in the given plane, but its projection onto the $x$-$y$ plane is not a circle - it is an ellipse.

Edit: The argument, however, can be made without any sort of reference to performing the actual coordinate integration.

Edit 2: You may also want to double check your computation of the curl.

 

[flyusx]

Your area is not $\pi$ as it should be the area in the $x$-$y$ coordinate plane. Your underlying problem is that what you call $\text{d}^{2}\textbf{r}$, the vector area element, is $\langle -1, -1, -1\rangle dx\, dy$, but the area covered in the $x$-$y$ plane by the relevant coordinate region is not $\pi$. The relevant curve is a circle in the given plane, but its projection onto the $x$-$y$ plane is not a circle - it is an ellipse.

Edit: The argument, however, can be made without any sort of reference to performing the actual coordinate integration.

Edit 2: You may also want to double check your computation of the curl.

Thanks. I re-evaluated the $z$-component to be zero (I accidentally wrote in an extraneous negative sign for 3x) and see that the circle is part of the surface so the area of interest is the 'projected ellipse' (please do correct me if my terminology is bad). I would therefore need to multiply the appropriate dot product (which is -8 instead of 2) by the area of the ellipse, correct?

 

[Orodruin]

Yes, but also note my first edit.

 

[flyusx]

You stated there isn't a need for coordinate integration, but I'm not too sure what this means. Does this mean integration is not necessary as in I can find the area of the ellipse without it? Or are you referring to the projection of a slanted circle?

 

[Orodruin]

Solve the problem any way you can manage first. Then we can discuss alternatives.

 

[flyusx]

Solve the problem any way you can manage first. Then we can discuss alternatives.

Thank you. Here's my solution which was confirmed to be right.

Since I got that the integral evaluated to -8 times the area of the ellipse, I wrote the answer as $-8\pi ab$ where $a$ and $b$ represent the major and semi-major axes. I used the attached diagram to evaluate the axis lengths. The major axis has a length of that of the radius of the circle.

To find the semi-major axis, I drew right triangle with the hypotenuse being the radius of the circle and one of the sides being a horizontal line (on the diagram, the line would be horizontal on the $\Pi_2$ plane passing through $S"$). The side length is the semi-major axis length and is the hypotenuse times the cosine of the angle $r\cos(\theta)$.

The angle formed is the angle between the $xy$ plane and the plane with the circle is the angle between the normal vectors of the planes. The $xy$ plane has an equation $z=0$ so the normal vector is $\langle0,0,1\rangle$. The normal vector of the plane with the circle is $\langle1,1,1\rangle$. Here: $$\textbf{a}\cdot\textbf{b}=\vert{\textbf{a}}\vert\vert{\textbf{b}}\vert\cos(\theta)$$ $$1=\sqrt{3}\cos(\theta)\rightarrow\cos(\theta)=\frac{1}{\sqrt{3}}$$
Hence the semi-major axis length is $\frac{1}{\sqrt{3}}$ since the radius is one. Then the integral evaluates to $$-8\pi ab=\frac{-8\pi}{\sqrt{3}}$$

 

[Orodruin]

Ok, good. Now, the easy way is to simply use that the area element is the unit surface normal multiplied by the infinitesimal area. Normalizing the vector $\langle 1,1,1\rangle$ gives a factor $1/\sqrt 3$ and the area of the circle of radius 1 is $\pi$. Hence $-8\pi/\sqrt 3$.