Strain Energy Functions and Springs

[Trying2Learn]

TL;DR

Strain energy and elastic constants: why is the strain energy formed this way

(If this is in the wrong forum, please move it)

Here is the potential energy of a spring

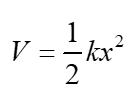
Here is the strain energy function in elasticity

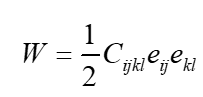
The look alike -- I like that.

If we want the force in the spring, we take the derivative of V with respect to the displacement and make the result NEGATIVE

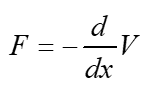
However, we note the following property of the strain energy function (from Fung's Solid Mechancis, page 128)

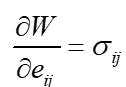
So, real stupid question: what happened to the negative?

I mean, I am trying to work my way through how elasticity, strain energy, etc. lead to the number of constants relating stress and strain. I will work this through on my own. I am trying to put all of this in some sort of contextual balance.

I can intuit the need for a strain energy function without the negative. But part of me wants to see the negative to make it harmonious with a spring.

Can someone get me out of this?

 

[Frabjous]

Try replacing the spring with a 1d bar. Upon extension, the bar experiences a tensile stress which produces a negative force on a point mass at the end of the bar/string.

The first equation looks at the force on a point mass. The force required to stretch the spring the relevant distance is the negative of this force.

 

[Trying2Learn]

Ah, of course. Thank you!