physics8553
So now we finally agree that electron neutrino tangles are chiral but not topologically chiral and that thus assigning zero electric charge makes sense. Phew, that took quite some time!
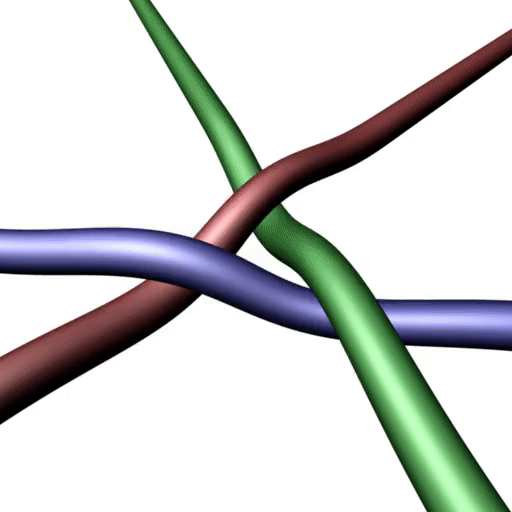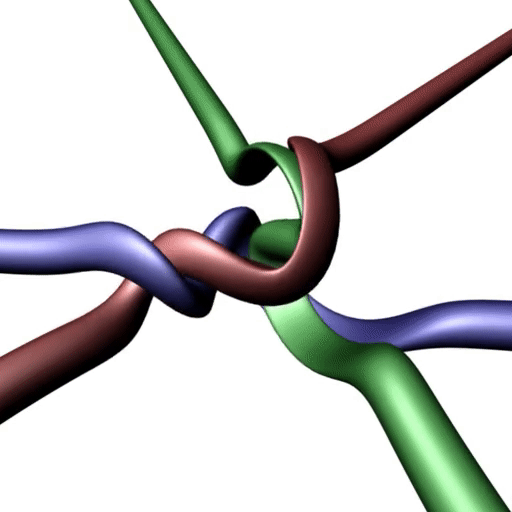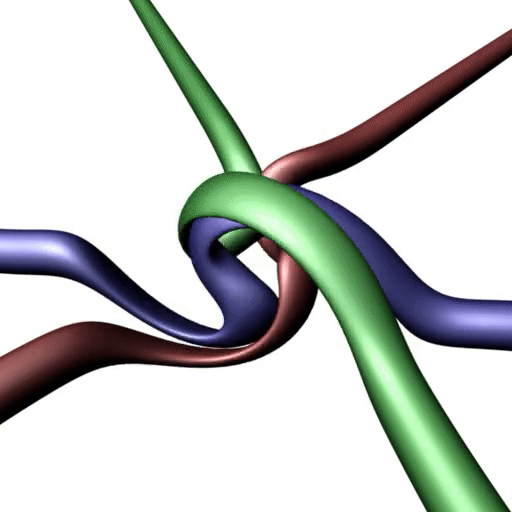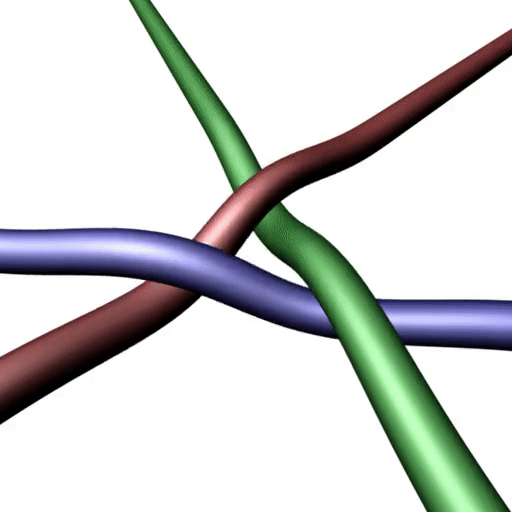
Now the next step. That is the electron tangle. Please draw it in Mathematica or make one with ropes.
There is no projection that has only two crossings. (You are obviously not allowed to shift crossings out of your field of view with the aim of not counting them.) The condition is that three ends/tethers are above and three ends /tethers below the paper plane, as set out in the definition. (And by the way, I do have three ropes to play near me.)
The mistake with the "MilkyWay" reasoning is that you are pushing crossings out of the MilkyWay by doing this. You have to count all crossings, not only the ones you like. When one says "locally", one has to look at the whole region that has crossings. This definition of "locally" is what corresponds to "locally" in usual physics. (If you want another definition, "locally" is that region which includes all curved sections of strands when you pull their ends.) The electron tangle is topologically chiral, in contrast to the electron neutrino tangle. That is why the electron is electrically charged.
Another topic you brought up: A photon tangle indeed has zero crossings in certain, even most projections; it is a single unknotted strand, after all. Any helix also has vanishing crossing number. The corkscrew model of the photon is old, and works well, if some additions (hopping) are made. And because the photon has zero crossing number, it has zero mass and zero electric charge. The labeling is consistent.
Just to be clear: Crossing number is a topological invariant. It is the number of crossings in the minimal projection. It is not the number of crossings in every projection. Electric charge in the chiral crossing number. That is another topological invariant. It is not the number of crossings in every projection. Many projections have more crossings than the minimal one.
Now the next step. That is the electron tangle. Please draw it in Mathematica or make one with ropes.
There is no projection that has only two crossings. (You are obviously not allowed to shift crossings out of your field of view with the aim of not counting them.) The condition is that three ends/tethers are above and three ends /tethers below the paper plane, as set out in the definition. (And by the way, I do have three ropes to play near me.)
The mistake with the "MilkyWay" reasoning is that you are pushing crossings out of the MilkyWay by doing this. You have to count all crossings, not only the ones you like. When one says "locally", one has to look at the whole region that has crossings. This definition of "locally" is what corresponds to "locally" in usual physics. (If you want another definition, "locally" is that region which includes all curved sections of strands when you pull their ends.) The electron tangle is topologically chiral, in contrast to the electron neutrino tangle. That is why the electron is electrically charged.
Another topic you brought up: A photon tangle indeed has zero crossings in certain, even most projections; it is a single unknotted strand, after all. Any helix also has vanishing crossing number. The corkscrew model of the photon is old, and works well, if some additions (hopping) are made. And because the photon has zero crossing number, it has zero mass and zero electric charge. The labeling is consistent.
Just to be clear: Crossing number is a topological invariant. It is the number of crossings in the minimal projection. It is not the number of crossings in every projection. Electric charge in the chiral crossing number. That is another topological invariant. It is not the number of crossings in every projection. Many projections have more crossings than the minimal one.