SUMMARY
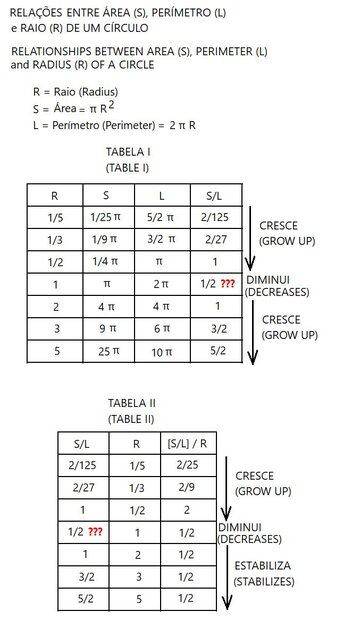
The discussion centers on the mathematical relationships between the area (S) and perimeter (L) of a circle, particularly how the ratios S/L and [S/L]/R vary with radius size (R). Key corrections were made regarding the perimeter values in the provided table, specifically that they should be 2/5π and 3/5π for the first two entries. The correct ratio S/L for R=1/2 is established as 1/4, not 1, highlighting the importance of unit consistency in mathematical expressions. The conversation emphasizes the need for accurate representation of geometric properties and encourages the use of appropriate symbols for clarity.
PREREQUISITES
- Understanding of basic geometry concepts, particularly circles and their properties.
- Familiarity with algebraic manipulation of formulas, specifically S = πR² and L = 2πR.
- Knowledge of dimensional analysis to differentiate between area and length units.
- Ability to interpret and correct mathematical tables and ratios.
NEXT STEPS
- Study the implications of the square-cube law on geometric shapes.
- Learn about dimensional analysis and its application in mathematical expressions.
- Explore the use of different symbols in mathematics for clarity and precision.
- Investigate common errors in mathematical tables and how to avoid them.
USEFUL FOR
Mathematicians, educators, students in geometry, and anyone involved in mathematical modeling or teaching who seeks to understand the relationships between geometric properties accurately.
 .
.