james_a
- 7
- 0
The problem:
So let's talk about part a.
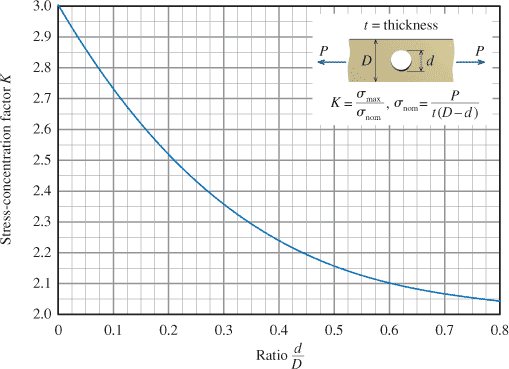
I understand that K=σmax/σnom. D is given as a constant, so K seems to be a function which will vary with d.
σnom is also a function which will vary with d
Now if an actual formula were given for K in terms of d and D, we would have one equation and one unknown, and I would know how to solve for that. We just have a picture of the plot of K though. So how does one go about it? It seems the only way to do this is basically to just guess a d value, look up K, calculate σmax, and see how close you are to the 150MPa. Is it really just that? Or is there a better way to do this?
Thanks in advance to anyone who can shed some light on this.
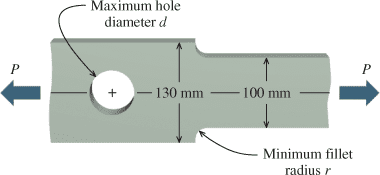
The stepped bar with a circular hole, shown in Figure P5.75, is made of annealed 18-8 stainless steel. The bar is 12-mm thick and will be subjected to an axial tensile load of P=70kN. The normal stress in the bar is not to exceed 150 MPa. To the nearest millimeter, determine
Given figures:(a) the maximum allowable hole diameter d.
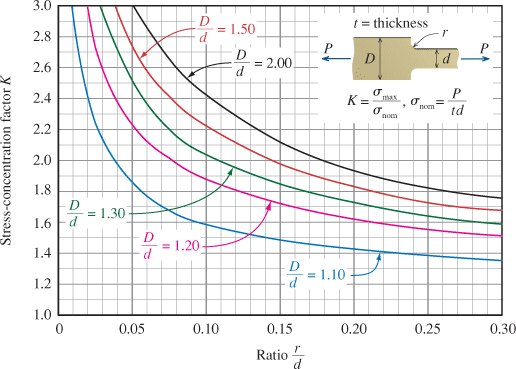
(b) the minimum allowable fillet radius r.
(b) the minimum allowable fillet radius r.
So let's talk about part a.
I understand that K=σmax/σnom. D is given as a constant, so K seems to be a function which will vary with d.
σnom is also a function which will vary with d
Now if an actual formula were given for K in terms of d and D, we would have one equation and one unknown, and I would know how to solve for that. We just have a picture of the plot of K though. So how does one go about it? It seems the only way to do this is basically to just guess a d value, look up K, calculate σmax, and see how close you are to the 150MPa. Is it really just that? Or is there a better way to do this?
Thanks in advance to anyone who can shed some light on this.