Satonam
- 38
- 1
Hello,
The resource I'm using is "Design of Machine Elements" by Spotts and, although they have examples of tensile and torsional stress, they don't show any examples with a load which causes a moment.
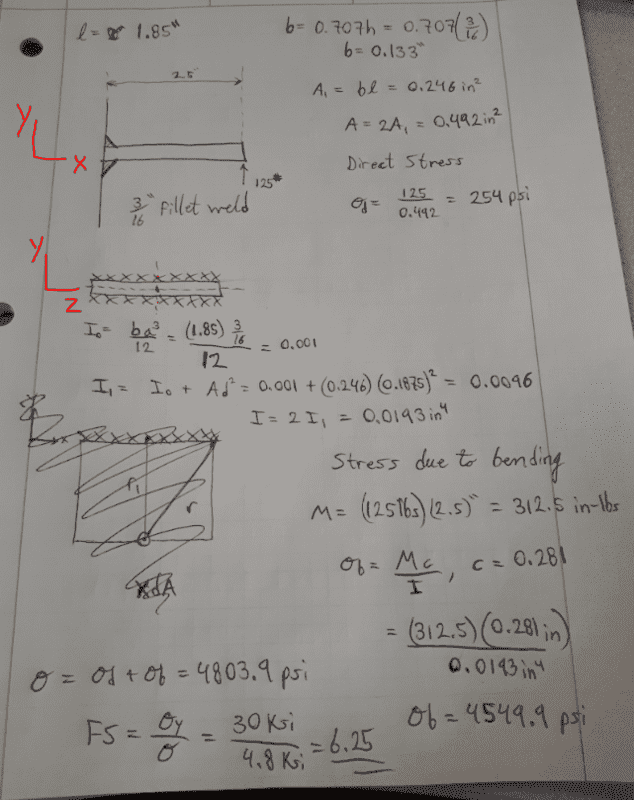
What we have here is web of 3/16" thickness and 1.85" depth welded onto a rigid body from both sides along its entire depth. In other words, 3/16" fillet welds with a 1.85" length. The 125 lb load is applied 2.5" from the weld.
My reasoning:
I calculated the direct stress by dividing the 125 lb load by the total throat area of the fillets. Next, I want to find the stress due to bending. Because the welds are on the same plane and symmetrical, the center of gravity of the weld group (cg) is located 3/32" into the thickness of the web. I then calculated the second moment of inertia of a single weld about its individual center of gravity (cgo), where b = length of weld = 1.85" and a = height of weld = 3/16", so,
Io = ba^3/12
Next, I used the parallel axis theorem to find the inertia at the center of gravity of both welds, where the distance between cg and cgo is d = 3/16"
I = Io + Ad^2
Due to symmetry, I is then multiplied by 2 to account for the second weldment.
Finally, the moment acting at the weld location M = (125 lbs)(2.5")
Stress due to bending is Mc/I, where c is the distance from cg to top of weld (c = 9/32")
Lastly, I added the direct stress to the bending stress. With a given yield stress, I calculated FS as usual.
Is this clear enough? Does my reasoning make sense?
If required, I can add better images later to clarify.
The resource I'm using is "Design of Machine Elements" by Spotts and, although they have examples of tensile and torsional stress, they don't show any examples with a load which causes a moment.
What we have here is web of 3/16" thickness and 1.85" depth welded onto a rigid body from both sides along its entire depth. In other words, 3/16" fillet welds with a 1.85" length. The 125 lb load is applied 2.5" from the weld.
My reasoning:
I calculated the direct stress by dividing the 125 lb load by the total throat area of the fillets. Next, I want to find the stress due to bending. Because the welds are on the same plane and symmetrical, the center of gravity of the weld group (cg) is located 3/32" into the thickness of the web. I then calculated the second moment of inertia of a single weld about its individual center of gravity (cgo), where b = length of weld = 1.85" and a = height of weld = 3/16", so,
Io = ba^3/12
Next, I used the parallel axis theorem to find the inertia at the center of gravity of both welds, where the distance between cg and cgo is d = 3/16"
I = Io + Ad^2
Due to symmetry, I is then multiplied by 2 to account for the second weldment.
Finally, the moment acting at the weld location M = (125 lbs)(2.5")
Stress due to bending is Mc/I, where c is the distance from cg to top of weld (c = 9/32")
Lastly, I added the direct stress to the bending stress. With a given yield stress, I calculated FS as usual.
Is this clear enough? Does my reasoning make sense?
If required, I can add better images later to clarify.
Last edited: