Superposition principle and information

[Virous]

I have a question about, perhaps, GCSE level physics, if not below, which, for some reason, is not explained anywhere I've looked up. Or, at least, I didn't find any explanation.

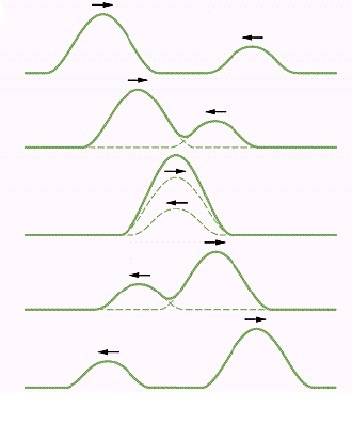The picture above is supposed to explain the concept of superposition. It depicts a pair of one-dimensional waves (wave pulses) at 5 different points in time. On the third picture (the exact moment of superposition), the initial individual waves do not exist. Instead we have a single large wave, composed of the energy of both. Where is the information about the shapes of the initial waves at this moment of time stored?

In other words, after the third picture, how does this large wave "know" how it should split in order to restore the initial pulses?

Thank you!

 

[phinds]

On the third picture (the exact moment of superposition), the initial individual waves do not exist.

I think that's where your problem lies. Both waveforms DO exist at that point exactly as they do exist at every other point on the graph, it's just that you are looking at the sum.

If you had a basket of 3 apples and you added 2 more apples, you wouldn't be thinking "damn, where did my 3 apples go? How can I get them out again?" but because the waveforms add in a smooth way, if you ONLY look at the waveform at that point in time, you can't tell what the individual waves look like, whereas with the apples you don't have that problem.

 

[Virous]

The apple example would make sense, since apples are composed of different matter (I mean, each apple has its own). The problem with waves, though, is that they are all made of the same matter (the same rope in this case, or whatever that is). So a wave is just a distribution of a particular property (in this case the displacement) in space/time.

When you add two numbers (e.g. 3 and 2) you get 5. If you give 5 to another person, he wouldn't be able to tell, if the original numbers were 4 and 1 or 3 and 2 or 2.5 and 2.5 and so on. This is exactly the same case :)

If you think of it in terms of particles, on the third picture one of the particles is "up" and it is ready to go down. How is that possible that when it goes down it gives unequal amounts of energy to absolutely identical particles on its left and right?

If I were to predict what's going to happen after, I would say that the resulting waves after the superposition would be equal. Yet, all the diagrams draw them in this way, so I'm confused.

 

[Virous]

Both waveforms DO exist at that point exactly

If the diagram depicts a real situation, they obviously do :) The question is, where? Particles definitely don't have this information, since they are just particles moving up and down and having a particular displacement function.

Suppose, I have managed to superimpose a million of waves with strange shapes (I guess I would need more dimensions, but anyway). Where will all this information go?