ocmaxwell
- 8
- 1
Hello all
I am trying to solve the following integral with Mathematica and I'm having some issues with it.
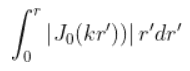
where Jo is a Bessel Function of first kind and order 0. Notice that k is a complex number given by
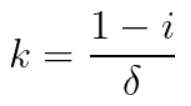
Where delta is a coefficient.
Due to the complex arguments I'm integrating the absolute value of the Bessel function.
I would like to solve the integral symbolically to get the result as a function or r, and not a number, so I can plot f(r) later on. See below what I did
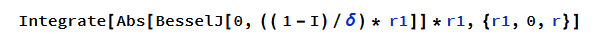 notice that r1 is r' in the integral above
notice that r1 is r' in the integral above
and the result

I am totally sure there should be a way in which it can be done.
Any help would be greatly appreciated
Thank you in advance
I am trying to solve the following integral with Mathematica and I'm having some issues with it.
where Jo is a Bessel Function of first kind and order 0. Notice that k is a complex number given by
Where delta is a coefficient.
Due to the complex arguments I'm integrating the absolute value of the Bessel function.
I would like to solve the integral symbolically to get the result as a function or r, and not a number, so I can plot f(r) later on. See below what I did
and the result
I am totally sure there should be a way in which it can be done.
Any help would be greatly appreciated
Thank you in advance