Symbolic integration of a Bessel function with a complex argument

[ocmaxwell]

Hello all

I am trying to solve the following integral with Mathematica and I'm having some issues with it.

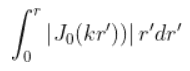
where Jo is a Bessel Function of first kind and order 0. Notice that k is a complex number given by

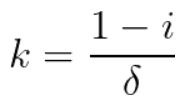
Where delta is a coefficient.

Due to the complex arguments I'm integrating the absolute value of the Bessel function.

I would like to solve the integral symbolically to get the result as a function or r, and not a number, so I can plot f(r) later on. See below what I did

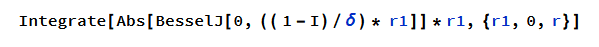notice that r1 is r' in the integral above
and the result

I am totally sure there should be a way in which it can be done.

Any help would be greatly appreciated

Thank you in advance

 

[Dale]

I am totally sure there should be a way in which it can be done

Usually if Mathematica doesn’t know a way then there is no known way.

 

[Bill Simpson]

This is certainly not a proof, but if you Plot3D the Re and the Im of either your Bessel or the Abs of your Bessel, say for {delta,-5,5} and {r1,-5,5} then that blowing up to infinity in lots of odd ways strongly hints to me that finding that integral might be really challenging. If you could restrict delta to being an integer, or even a specific integer, then the graphs hint that might possibly be a simpler problem. Without giving Mathematica any information about delta it will proceed imagining that delta might even be complex

 

[ocmaxwell]

You are very right Mr. Simpson
For this case delta is real, how could I enforce this condition so mathematica undertands it and still gives me the result of the integral in terms of delta and r?

Thank you for your response

 

[Dale]

You can use the option “Assumptions” to tell it to assume that it is real.

 

[ocmaxwell]

Thank you Sir, I will try that out.
Thank you for taking the time to respond.