CSteiner
- 31
- 0
I have an extremely messy system of differential equations. Can anyone offer any ideas for a general solution?
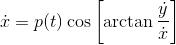
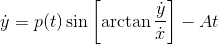
p(t) is a function of t, and A is a constant.
p(t) is a function of t, and A is a constant.