Sagrebella
- 61
- 2
Member advised to use the homework template for posts in the homework sections of PF.
Hello,
One more question, this time it's about projectile motion. Could someone please check my answer to this problem. All my work and applicable equations are shown in the pictures below. If my answer is wrong, please provide me with guidelines for solving the problem. I'm not expecting anyone to just give me the answer :)
Thanks
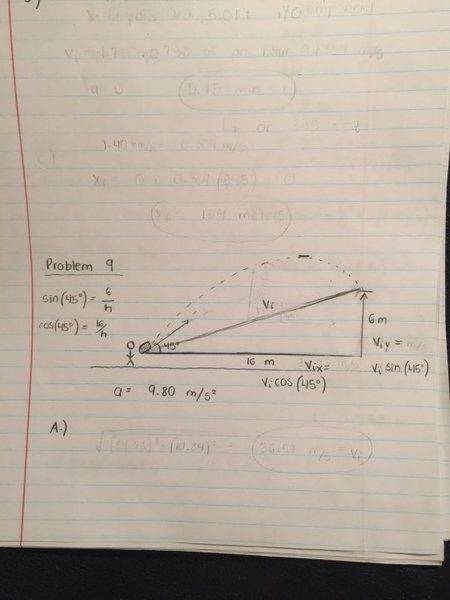
Problem 9
You're attending a professional basketball game. The home team calls timeout, and, as the music gets cranked up, the t-shirt crew comes out onto the floor to fire team t-shirts into the crowd. Like everyone else, you stand up and wave your arms wildly, hoping that one of the t-shirt guys will fire a shirt your way. The t-shirts are fired from a launcher that uses compressed air. One of the launchers is pointed your way, and is just about to launch a t-shirt at a 45° angle from the horizontal. You are a horizontal distance of 16.0 m from the launcher and a vertical distance of 6.00 m above it. Neglect air resistance, and assume that the acceleration due to gravity is 9.80 m/s2.
(a) What is the launch speed needed so that the t-shirt reaches you, rather than one of the hordes of people sitting near you?
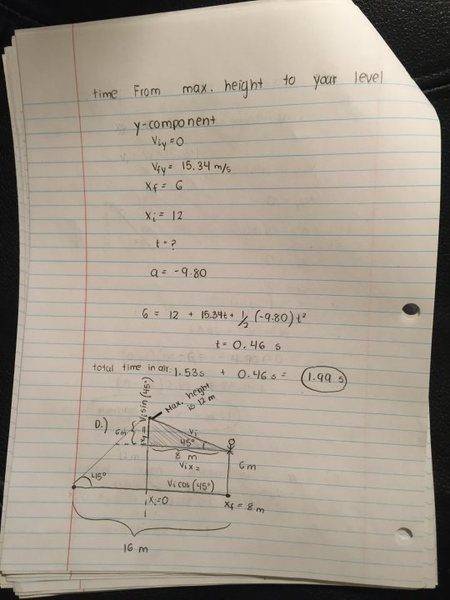
(b) What is the maximum height reached by the t-shirt (measured from the level of the launcher)?
(c) How long does the t-shirt spend in the air before reaching you?
(d)What is the speed of the t-shirt when it reaches you?
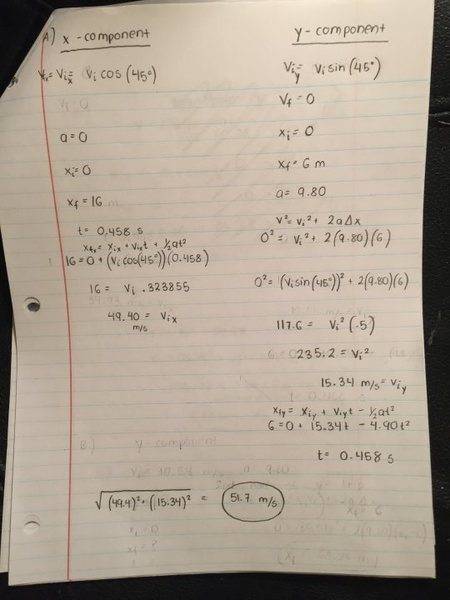

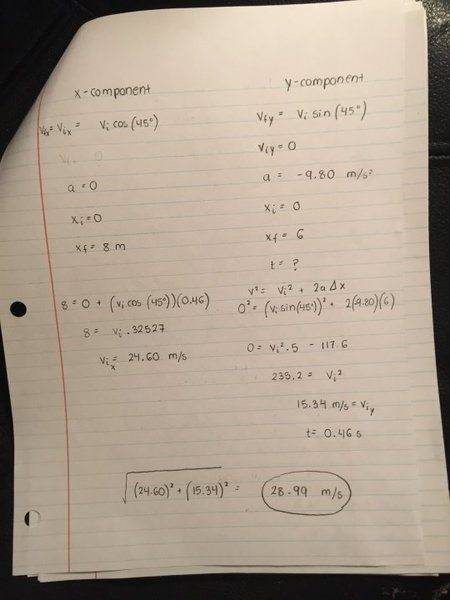
One more question, this time it's about projectile motion. Could someone please check my answer to this problem. All my work and applicable equations are shown in the pictures below. If my answer is wrong, please provide me with guidelines for solving the problem. I'm not expecting anyone to just give me the answer :)
Thanks
Problem 9
You're attending a professional basketball game. The home team calls timeout, and, as the music gets cranked up, the t-shirt crew comes out onto the floor to fire team t-shirts into the crowd. Like everyone else, you stand up and wave your arms wildly, hoping that one of the t-shirt guys will fire a shirt your way. The t-shirts are fired from a launcher that uses compressed air. One of the launchers is pointed your way, and is just about to launch a t-shirt at a 45° angle from the horizontal. You are a horizontal distance of 16.0 m from the launcher and a vertical distance of 6.00 m above it. Neglect air resistance, and assume that the acceleration due to gravity is 9.80 m/s2.
(a) What is the launch speed needed so that the t-shirt reaches you, rather than one of the hordes of people sitting near you?
(b) What is the maximum height reached by the t-shirt (measured from the level of the launcher)?
(c) How long does the t-shirt spend in the air before reaching you?
(d)What is the speed of the t-shirt when it reaches you?
