Tangent slope with polar coordinate

[yecko]

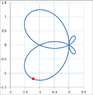
Homework Statement

http://i.imgur.com/4FPnTNS.jpg

Homework Equations

(Written in above photo)

The Attempt at a Solution

(Written in above photo)

I have tried hard in figuring out what's wong I have done done, but what I finally got is still option d instead of the model answer e.
Are there any bugs and where are they?
Thank you very much.

(Please forgive me for writing out all the thing because of the difficulty in typing all those expressions.)

 

[BvU]

How much is $-{1\over 2} -{1\over 2}$ ?

 

[yecko]

How much is $-{1\over 2} -{1\over 2}$ ?

It is -1 which I forgot to change in the last line of the step, but I have corrected it in the following steps already... It shouldn't be a problem to the answer...

Whats other bug? thank you.

 

[ehild]

It is -1 which I forgot to change in the last line of the step, but I have corrected it in the following steps already... It shouldn't be a problem to the answer...

Whats other bug? thank you.

Try to draw the curve r=f(θ). Is θ=pi/4 in the domain?

 

[BvU]

I have corrected it in the following steps already... .

No you haven't.

 

[BvU]

Try to draw the curve r=f(θ). Is θ=pi/4 in the domain?

[EDIT]Typo. I see what you mean -- and what the exercise composer means

 

[ehild]

The polar coordinate r can not be negative as it is the distance from the origin.Half of your curve resulted from negative r=f(θ). The problem maker forgot about that.

 

[John Park]

(Edit)
Unless I blundered, it looks quite tractable if you start by transforming to cartesian co-ordinates.

Edit: I did and it isn't