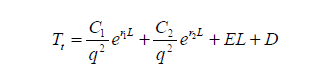Temperature Profile Function: T(L) for 0-500 Depth

  • Context: MHB 
  • Thread starter Thread starter mk747pe
  • Start date Start date
  • Tags Tags
    Function
Click For Summary
SUMMARY

The discussion centers on creating a temperature profile function T(L) based on depth L, which varies from 0 to 500. User mk747pe inquired about plotting this function, and another participant confirmed that T(L) is already defined and can be graphed by substituting numerical values for constants. The example provided involved using constants of $1$ and $-1$ to demonstrate how to visualize the function effectively. The inquiry was resolved satisfactorily, confirming the user's understanding and needs.

PREREQUISITES
  • Understanding of mathematical functions and graphing techniques
  • Familiarity with the concept of temperature profiles in scientific contexts
  • Basic knowledge of variable manipulation in equations
  • Experience with graphing software or tools for visualizing functions
NEXT STEPS
  • Explore graphing tools such as Desmos or GeoGebra for visualizing mathematical functions
  • Learn about temperature profile modeling in environmental science
  • Investigate how to manipulate and analyze functions in Python using libraries like Matplotlib
  • Study the implications of different constants in temperature equations and their effects on graph shape
USEFUL FOR

Students, researchers, and professionals in environmental science, mathematics, and engineering who are interested in modeling and visualizing temperature profiles based on depth.

mk747pe
Messages
4
Reaction score
0
Hello,

so I have equartion for temperature profile (T) based on depth (L),
View attachment 7594

L will vary let's say from 0 to 500 and I want to create a function dependent on T and L, so I can plot a graf.
 

Attachments

  • Bez názvu.png
    Bez názvu.png
    1.6 KB · Views: 111
Physics news on Phys.org
mk747pe said:
Hello,

so I have equartion for temperature profile (T) based on depth (L),L will vary let's say from 0 to 500 and I want to create a function dependent on T and L, so I can plot a graf.

Hi mk747pe,

What you have is already a function T(L).
If we fill in some numbers, we can graph it.
See for instance here, where I filled in $1$ or $-1$ for every constant, and I picked a range for $L$ such that we see a reasonable graph.

Or did you have something else in mind? (Wondering)
 
I like Serena said:
Hi mk747pe,

What you have is already a function T(L).
If we fill in some numbers, we can graph it.
See for instance here, where I filled in $1$ or $-1$ for every constant, and I picked a range for $L$ such that we see a reasonable graph.

Or did you have something else in mind? (Wondering)

Thats exactly what I needed. Thank you very much.
Problem solved :)
 

Similar threads

Graduate Fourier series approximation of a discontinuous eddy function
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Conservation of Mass for Compressible Flow
  • · Replies 33 ·
2
Replies
33
Views
4K
High School Question about units for "area under curve"
  • · Replies 2 ·
Replies
2
Views
3K
Undergrad Creating a function with specific shape, intercepts, integral....
  • · Replies 1 ·
Replies
1
Views
1K
Undergrad On (real) entire functions and the identity theorem
  • · Replies 2 ·
Replies
2
Views
3K
Undergrad Question about uniform convergence in a proof
  • · Replies 1 ·
Replies
1
Views
3K
High School How do I invert this exponential function?
  • · Replies 3 ·
Replies
3
Views
4K
High School Another proof of the existence of extreme values on open intervals
  • · Replies 9 ·
Replies
9
Views
2K
Undergrad Some questions on l'Hôpital rules
  • · Replies 9 ·
Replies
9
Views
3K
Chemistry Understanding thermodynamics of a stretched rubber band
  • · Replies 2 ·
Replies
2
Views
2K