xorg
- 15
- 0
Hi. I'm reading the bookhttp://amzn.com/0486649407 ,

in self-study mode.
In page 53 and 54, below:
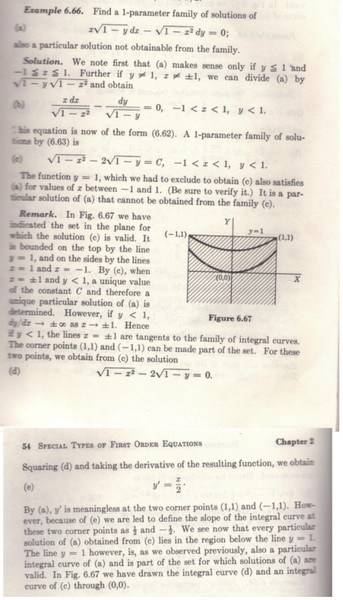
Apparently does not make sense, because, If the differential equation is:
$$ \frac{\mathrm{d}y }{\mathrm{d} x} = x\frac{\sqrt{1-y}}{\sqrt{1-x^{2}}} $$
then dy/dx = ∞ when x = 1, and y < 0
however, in Image:
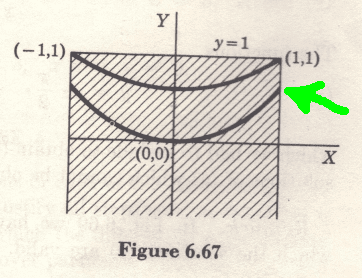
dy / dx is not ∞ in point marked in green.
Then, in this point, the graph changes radically the slope? Apparent, does not make sense, It seems that the correct curve would go up until tangent to x = 1, while the particular solution says otherwise.
Why the differential equation "fails", and the solution of the differential equation not? I did not catch that.
I am studying alone, thank you for your patience.
in self-study mode.
In page 53 and 54, below:
Apparently does not make sense, because, If the differential equation is:
$$ \frac{\mathrm{d}y }{\mathrm{d} x} = x\frac{\sqrt{1-y}}{\sqrt{1-x^{2}}} $$
then dy/dx = ∞ when x = 1, and y < 0
however, in Image:
dy / dx is not ∞ in point marked in green.
Then, in this point, the graph changes radically the slope? Apparent, does not make sense, It seems that the correct curve would go up until tangent to x = 1, while the particular solution says otherwise.
Why the differential equation "fails", and the solution of the differential equation not? I did not catch that.
I am studying alone, thank you for your patience.
Last edited by a moderator: