Tension measured by a voltmeter of given bottom scale and current range

[greg_rack]

Homework Statement

For measuring tension, a voltmeter uses a part of the current flowing through the circuit.
Subsequently, the tension measured is just an approximation of the one present when the voltmeter is not connected.
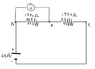
Consider a circuit formed by two $1550\Omega$ resistors connected in series powered by a $60.0V$ battery:
\rightarrow Find the tension of the two resistors.

An analogic voltmeter has a bottom scale of $60.0V$ and uses a galvanometer with a maximum current range of $5.00mA$:
\rightarrow Find the tension measured by this voltmeter when it's connected to the ends of the resistors.

Relevant Equations

$I=\frac{V}{R}$

First and foremost, I've studied voltmeters and ammeters on my own, and online there aren't many resources to do so... forgive me in advance for eventual silly questions/doubts :)

I managed to calculate(intuitively) a tension of $30.0V$ per resistor, with basic procedures.

However, I'm finding difficulties in solving the second point.
What does the "bottom scale" mean? Isn't it simply the maximum tension that can be measured by this tool? Also, how should I use the "maximum current range" data?
Lastly: If the voltmeter must be precise, how could this result be different from that calculated in the first point?

 

[haruspex]

What does the "bottom scale" mean?

Many voltmeters and ammeters have a second scale, usually the upper one, used for some other purpose. Don't worry about it.

how should I use the "maximum current range" data?

I believe that would be the current through the galvanometer at max deflection.

 

[greg_rack]

I believe that would be the current through the galvanometer at max deflection.

And how could I apply it to my specific case? How do I know the current flowing through the galvanometer?

I still don't understand that if the voltmeter must be precise, how could the result of the 2nd point be different from that calculated in the first point? (it's 28.1V instead of 30V)

 

[haruspex]

How do I know the current flowing through the galvanometer?

It tells you that if the voltmeter reads 60V then the current through it is 5mA.
So what is the resistance of the galvanometer?

Draw a circuit diagram showing the three resistances. With 60V applied, what will the galvanometer read?

 

[greg_rack]

It tells you that if the voltmeter reads 60V then the current through it is 5mA.

Oh ok then, now it's clear! The internal resistance is going to be $R_{G}=\frac{60V}{5\cdot 10^{-3}A}$

Draw a circuit diagram showing the three resistances. With 60V applied, what will the galvanometer read?

so, this is my circuit
Considering the internal resistance of the galvanometer, it will "absorb" a current of $I_{G}=\frac{60.0V}{R_{G}}$, which will be subtracted to that one flowing through the resistor... so it will measure a voltage $V=(I_{initial}-I_{G})\cdot 1550\Omega$.
Does it make any sense?

 

[haruspex]

View attachment 271902so, this is my circuit
Considering the internal resistance of the galvanometer, it will "absorb" a current of $I_{G}=\frac{60.0V}{R_{G}}$,

Is the voltage across it 60V?
What current will flow around the circuit?

 

[greg_rack]

Is the voltage across it 60V?

Right, the voltage across it is 30V.

What current will flow around the circuit?

Do you mean the current with or without the galvanometer applied? Which of the two is relevant?

 

[greg_rack]

Do you mean the current with or without the galvanometer applied? Which of the two is relevant?

Auto-quote: I've managed to solve the problem applying Kirchhoff's 2nd law, @haruspex:

 

[haruspex]

Auto-quote: I've managed to solve the problem applying Kirchhoff's 2nd law, @haruspex:View attachment 271919

Well done.