Grizzly_1
- 7
- 3
- Homework Statement
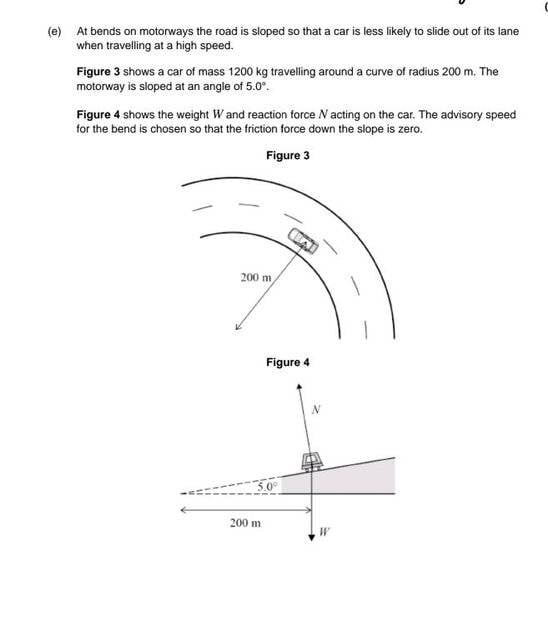
- At bends on motorways the road is sloped so that a car is less likely to slide out of its
lane when travelling at a high speed.
Figure 7 shows a car of mass 1200 kg travelling around a curve of radius 200 m.
The motorway is sloped at an angle of 5.0°.
Figure 8 shows the weight W and reaction force N acting on the car. The advisory
speed for the bend is chosen so that the friction force down the slope is zero.
Suggest an appropriate advisory speed for this section of the motorway
- Relevant Equations
- F=mv^2/r
Hello all, I am sadly stuck on the last part of a circular motion question sheet I was given for homework. I have a mark-scheme with me, but it has actually given me more questions than answers. I have attached my working, and how I arrived at my answer, and the differences it has with the mark-scheme answer. To note, the mark-scheme answer rounds to my answer, but the trigonometry they used is entirely opposite to mine. I would really appreciate some help in understanding:

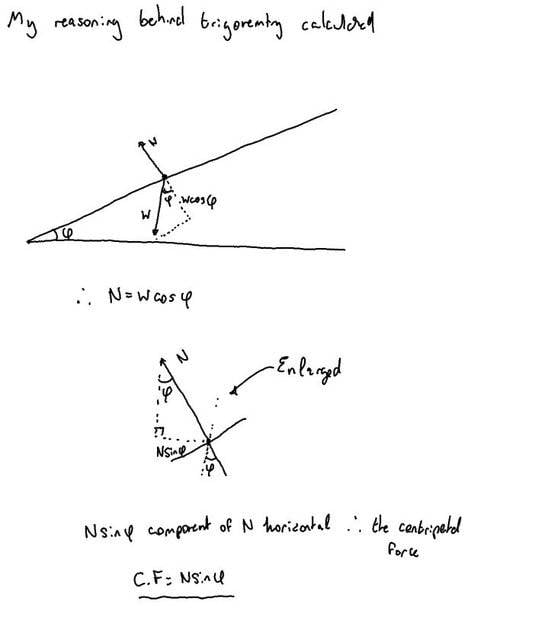
Thanks to anyone who can lend me a hand on this. I assume it is just poor physics on my end, so getting through this will help keep me up to scratch on circular motion.
Thanks to anyone who can lend me a hand on this. I assume it is just poor physics on my end, so getting through this will help keep me up to scratch on circular motion.