The Curvature of the Earth

[FelixLudi]

(i.e the height you need to be at to look forward)
(This isn't in physics subforum because it's more of a geometry question, this is NOT a homework question and it's more of a random thought)

Basically, I've been thinking what height would you have to be at, to see 1° of Earth's curvature.
So this is my math;

Circumference of Earth = 40.075 km ~ 40 000 km
x = 40 000 km

Assuming that Earth is a perfect sphere, and that in 2D it's a perfect circle it's angle would be 360°.

Over 1° of Earth's curvature, the distance (d = x/360°)
d = 40000 km / 360°
d = 111,11* km
(In my school we put an asterisk at the end to define a number without end (e.g 2/3 = 0.66*))

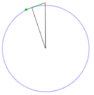
Over that 1° of curvature, I assumed a shape of a triangle where the ground points are defined as dots A and B where the dot A has almost a sharp angle (90°) and the dot B has an angle of 1°.
In that triangle the cathetus between A and B is equal to d = 111,11* km, and the dot C which is elevated above dot A has the other cathetus of undefined height a, while the hypotenuse is c and is directly opposite of the dot A. In this triangle the hypotenuse and the cathetus d are near the same length, and I can not go further than this to calculate the height a needed to look over from dot A to dot B over the Earth's curvature (angle) of 1°. How do I adjust the equation of Pythagoras' theorem to this triangle?

Anyone that can help me?
Thanks!

 

[mfb]

(In my school we put an asterisk at the end to define a number without end (e.g 2/3 = 0.66*))

How would you distinguish 5/11 = 0.454545... from 0.4+5/90 = 0.455555...?
Anyway, it is better to round to useful values, if you need numerical values. The circumference is not exactly 40,000 km.

Over that 1° of curvature, I assumed a shape of a triangle where the ground points are defined as dots A and B where the dot A has almost a sharp angle (90°) and the dot B has an angle of 1°.

Where are A and B? As seen from the surface, the other surface point is not 1 degree below the horizontal.

You probably want to consider a triangle that involves the center of Earth.

 

[FelixLudi]

How would you distinguish 5/11 = 0.454545... from 0.4+5/90 = 0.455555...?

Technically we put asterisks above the said number, if it were 0.4545 we would put asterisks above 4 and 5 (0.4*5* where the asterisks are actually above said numbers). And if it were 0.4555 we would just put one asterisk on the 5.
Kinda hard to explain but I assume you get the point.

Where are A and B? As seen from the surface, the other surface point is not 1 degree below the horizontal.

Assuming to the calculation, from point A to point B there should be approximately 111.11 km (distance d) between them, including 1° of curvature and assuming the Earth is a perfect sphere, and that it's circumference is exactly 40 000 km.

You probably want to consider a triangle that involves the center of Earth.

What did you mean by that?
A triangle that starts in the center of the Earth, in which point it has a 1° angle and that extends to the surface?
Seems plausible, but I'm looking for the height needed to look over 1° of curvature of the Earth.

 

[Janus]

Technically we put asterisks above the said number, if it were 0.4545 we would put asterisks above 4 and 5 (0.4*5* where the asterisks are actually above said numbers). And if it were 0.4555 we would just put one asterisk on the 5.
Kinda hard to explain but I assume you get the point.Assuming to the calculation, from point A to point B there should be approximately 111.11 km (distance d) between them, including 1° of curvature and assuming the Earth is a perfect sphere, and that it's circumference is exactly 40 000 km.What did you mean by that?
A triangle that starts in the center of the Earth, in which point it has a 1° angle and that extends to the surface?
Seems plausible, but I'm looking for the height needed to look over 1° of curvature of the Earth.

Something like this

The green line is your sight line which just grazes the horizon from your position at the top of the red line. Just solve for the triangle for the desired angle between the two black lines and find the length of the red line from that.

 

[FelixLudi]

Something like this
View attachment 221535
The green line is your sight line which just grazes the horizon from your position at the top of the red line. Just solve for the triangle for the desired angle between the two black lines and find the length of the red line from that.

How would I get the length of the green line and how would I encorporate that into the given formula.
So far the only thing I can understand is that the black lines are equal to Earth's radius (r = 6 371 km).
The left black line is equal to r but the right line also has the red line, so it would be higher.
How do I solve for the desired angle, I doubt that Pythagoras' theorem would work for angles.

 

[mfb]

The tangent function will help here.
If you don't know that yet: The length of the green line is approximately 111 km, you can determine the length of the red line with Pythagoras alone using this approximation.

 

[FelixLudi]

Yes but I do not know where to include the angle in the a² + b² = c² formula.

 

[Janus]

Yes but I do not know where to include the angle in the a² + b² = c² formula.

You don't. You use trigonometry.
The triangle has three sides:
The hypotenuse (combined black and red line)
Adjacent ( the "black only" line)
And the opposite ( the green line).
Cos(A) = Adjacent/hypotenuse
Thus, using your calculator, find the cos of the angle you are interested in (A).
Divide the length of the adjacent side (equal to the radius of the Earth) by this.
This gives you the length of the hypotenuse. From which you can get the length of the red line.

 

[FelixLudi]

You don't. You use trigonometry.
The triangle has three sides:
The hypotenuse (combined black and red line)
Adjacent ( the "black only" line)
And the opposite ( the green line).
Cos(A) = Adjacent/hypotenuse
Thus, using your calculator, find the cos of the angle you are interested in (A).
Divide the length of the adjacent side (equal to the radius of the Earth) by this.
This gives you the length of the hypotenuse. From which you can get the length of the red line.

I understand how I would use Cos there but the red line is included in the hypotenuse, and I need to calculate the red line using the hypotenuse (which includes it)?
Saying that the adjacent is b and the hypotenuse is c, in which c₁ is the radius of the Earth (the black line in the hypotenuse) and c₂ is the red line in the hypotenuse. (c = c₁ + c₂).
Therefore to calculate the Cos of A;
Cos(A) = b / c
Cos(A) = b / (c₁ + c₂)
Cos(A) = 6371 km / (6371 km + c₂)

Or did I misunderstand?

 

[jbriggs444]

If you've already calculated A then you calculate the cosine of A by keying A into your calculator and hitting the cos key.

 

[Janus]

I understand how I would use Cos there but the red line is included in the hypotenuse, and I need to calculate the red line using the hypotenuse (which includes it)?
Saying that the adjacent is b and the hypotenuse is c, in which c₁ is the radius of the Earth (the black line in the hypotenuse) and c₂ is the red line in the hypotenuse. (c = c₁ + c₂).
Therefore to calculate the Cos of A;
Cos(A) = b / c
Cos(A) = b / (c₁ + c₂)
Cos(A) = 6371 km / (6371 km + c₂)

Or did I misunderstand?

As alluded to by jbriggs444, Cos(A) is a known since you already know what A is (in this case 1°) Today, you just use a calculator, and in pre-calculator days you'd look it up on a trig table or use a slide rule.

Thus in the equation, you just rearrange until your one unknown is one side by itself.
$$c_2 = \frac{b}{\cos A}-c_1$$

and since c₁= b
$$c_2 = \frac{b}{\cos A}-b$$

$$c_2 = b \left ( \frac{1}{\cos A} -1 \right )$$

Now if A is small, as it is here, and you don't need an exact answer you can get a close answer through the method aluded to by mfb in post #6

For small values of A, the Green line (a) is almost the same as the distance along the surface of the Earth between the hypotenuse (c) and the radial line b.
Thus this distance will be ~b (pi/180) in length if A = 1°
This gives us two sides of the triangle a and b, and we now can find the hypotenuse c, subtract b from it to get c₁
For different values of A the arc length becomes ~ bA( pi/180)
And with a bit of algebra we can arrive at the equation:
$$c_2 = b \left ( \sqrt { \left ( \frac{A \pi}{180} \right) ^2 +1}-1 \right )$$

But as I said above, this only gives a reasonably close answer if A is small.

Here is the graph comparing the two methods for values of A from 1° to 45°

The blue line is from the Trig solution and the red line from the Pythagorean theorem approximation.