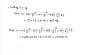The motion of a particle is defined by the relation

[Alexanddros81]

Homework Statement

The motion of a particle is defined by the relation $x = 6t^4 - 2t^3 - 12t^2 + 3t + 3$, where
x and t are expressed in meters and seconds, respectively. Detrmine the time, the position,
and the velocity when a = 0.

Homework Equations

The Attempt at a Solution

[/B]
Can you check my solution?

 

[dRic2]

The method is correct, and I trust you on the calculations

 

[kuruman]

As you have found, the acceleration is also zero at the earlier time t = - 0.5 s. There is no compelling reason to exclude this time from the calculations. At t = 0 the particle is at x = 3 m moving with velocity v = 3 m/s and must be coming from somewhere. Equations in physics are often used to figure out what went on in the past based on what's going on in the present.

 

[Alexanddros81]

Hi.

I have calculated v and x for when time is -0.5 also.

Well Beer gives the solutions only for when time is 2/3. Why is that?

 

[kuruman]

Well Beer gives the solutions only for when time is 2/3. Why is that?

Because he wrote the problem and knows what's on his mind better than I do.