The physics behind mixing coloured pigments (questions inside post)

[TomP86]

Hi all. My question is regarding the mixing of 2 pigments (such as paints) to form a uniform colour in the retina.

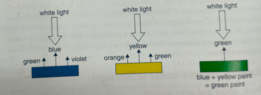
I understand mixing yellow and red create orange. This can be easy seen as red pigment will reflect a little orange light and yellow pigment will reflect a little orange light indevidually (where they are not mixed), so during the subtraction of mixing them together, the orange is the colour in common they both reflect so the eye precieved it as orange.

Simmilar, mixing yellow and blue yeilds the same result making it green with in the wave length inbetween yellow and blue.

What I am having some difficulty with is the mixing of red (780nm) with blue(450nm). There is no common reflected colour as scene in the 2 examples above (Y and O, and B and Y). Im trying to understand how our mind precieves this colour as purple.

From online searching it seems to be a biological answer based on the RGB photoreceptor cones in our eyes.

If I followed the proceedure above for calculating a mixture of red and blue it would result in black as there is no common reflected colour. But this is clearly not the case.

So when you mix 2 pigments together, what actually happens. Do the molecule from the first pigment mix together (at seeminly random) with the second pigments molecues and as the light wave reflects from each individule (separate pigment molecule) it reflects the light that that particular pigment molocule does not obsorb?

or is there a chemical reaction that bonds the 2 pigments? (My chestry knolwege is limited at the moment). And if so, what wavelength will the bonded molecule reflect?

If the answer is the former, (the surface with the mixed pigment reflects a proportion of wave pigments 1's reflecetive wavelength and of pigments 2's reflective wavelength depending on the ratio quantity that was mixed), then the perception of the purple is a color calculated by the human mind? Or is there a physical explaination?

Thank you very much in advance,

Yours Tom P.

 

[Drakkith]

I understand mixing yellow and red create orange. This can be easy seen as red pigment will reflect a little orange light and yellow pigment will reflect a little orange light indevidually (where they are not mixed), so during the subtraction of mixing them together, the orange is the colour in common they both reflect so the eye precieved it as orange.

While this may happen to some extent, the main reason it looks orange is because of the way the eye and brain process colors. In short, the red and yellow pigments excite your cone cells in your eyes in such a way as to cause you to perceive it as orange. The same for purple. See here for more: https://en.wikipedia.org/wiki/Color_vision#Physiology_of_color_perception

So when you mix 2 pigments together, what actually happens. Do the molecule from the first pigment mix together (at seeminly random) with the second pigments molecues and as the light wave reflects from each individule (separate pigment molecule) it reflects the light that that particular pigment molocule does not obsorb?

or is there a chemical reaction that bonds the 2 pigments? (My chestry knolwege is limited at the moment). And if so, what wavelength will the bonded molecule reflect?

The former. Each pigment reflects its own spectrum, the combination of which gives the overall material its color.

 

[Baluncore]

Welcome to PF.

Our eyes have cones that detect three different colour bands. The presence of more red and blue, than yellow or green, appears to us as what we call purple.
https://en.wikipedia.org/wiki/Color_vision#Physiology_of_color_perception

 

[TomP86]

Thank you for the reply guys. To help clarfy my question better Im trying to ask why do our eyes precieve the presense of only 2 wavelengths (red and blue) as purple.

In my physics book there is a concept of 'impure colour' whereby 2 (or more) different wavelengths of colour are interpreted in our mind or retina (not sure which) as an average of the 2 or more colours. eg. red and green (700nm and 540nm respectivly) average to make 620nm (yellow). So our eyes see the object as yellow (simmilar to how a tv works)

So in the case of red and blue we have 700nm and 480nm respectivley and an average of 590 which is an orange colour. So why is it purple?

After doing some research I found the answer I believe and it is due to the strange way our receptors work (they are not perfect bell curves)

Credit to yeti on stackexchange as he found the answer. I think 20 years ago I actually learnt this but I've forgotten now. The L receptor is more absorbing on the lower wavelengths for colours whereby the violet wavelength area is so if we mixed red from the L and some of the M receptors with this we replicate the purple colour scene in accordance to this graph. The answer is our retiners interpret things with a spceicifc way as represented in this graph

Based on the graph above a colour chart can be drawn describing how the receptors perceive light based on different proportions on each receptor. This chart can show you how to fix what colour is produced by each wavelength and what colour can be produced by mixing different wavelengths in different proportions. For a full really good explanation, just read this post

 

[sophiecentaur]

There is no common reflected colour as scene in the 2

If there is no common reflected colour then the result will be black . This is why the primaries for mixing pigments (subtractive mixing) are Cyan, Magenta and Yellow which, as you may remember are the product of additive colour mixing of, respectively Blue plus green, Red plus blue and Red plus green. If you use 'perfect' Red Green and Blue Pigments, the results will always be a dark result or black.
Your TV primary elements are RGB and your printer inks are CMY so that proves my point.
Also, C is often referred to as -R, M is referred to as -G and Y is referred to as -B. There are practical reasons why the detailed reflection spectra of the pigments are chosen the way they are is that you still want bright, saturated colours, which subtractive mixing militates against so there are compromises. In particular, if you want really good matches for some familiar colours (e.g.Coca cola Red) high quality printing uses extra 'spot' colours in addition to three colour printing. TV (additive) mixing is much less hassle whereas old Cinema film had really rubbish colourimetry. They got away with it in darkened cinemas because eyes adapted and learned to ignore the poor colour.