The precession of Mercury's orbit

[PainterGuy]

TL;DR Summary

Does the precession of Mercury's orbit change the plane of its orbit?

Hi,

I was reading about the general relativity to get some basic understanding and it was said that the proper answer to problem of precession of Mercury was provided by the general relativity. Then, I started reading about the precession of Mercury orbit.

"Mercury deviates from the precession predicted from these Newtonian effects. This anomalous rate of precession of the perihelion of Mercury's orbit was first recognized in 1859 as a problem in celestial mechanics, by Urbain Le Verrier. His reanalysis of available timed observations of transits of Mercury over the Sun's disk from 1697 to 1848 showed that the actual rate of the precession disagreed from that predicted from Newton's theory by 38″ (arc seconds) per tropical century (later re-estimated at 43″ by Simon Newcomb in 1882).[6] A number of ad hoc and ultimately unsuccessful solutions were proposed, but they tended to introduce more problems.

In general relativity, this remaining precession, or change of orientation of the orbital ellipse within its orbital plane, is explained by gravitation being mediated by the curvature of spacetime. Einstein showed that general relativity[3] agrees closely with the observed amount of perihelion shift. This was a powerful factor motivating the adoption of general relativity." - https://en.wikipedia.org/wiki/Tests_of_general_relativity#Perihelion_precession_of_Mercury

Note to self:
"A minute of arc, arcminute (arcmin), arc minute, or minute arc is a unit of angular measurement equal to 1/60 of one degree. Since one degree is 1/360 of a turn (or complete rotation), one minute of arc is 1/21600 of a turn. ... A second of arc, arcsecond (arcsec), or arc second is 1/60 of an arcminute, 1/3600 of a degree, 1/1296000 of a turn, and π/648000 (about 1/206265) of a radian." - https://en.wikipedia.org/wiki/Minute_and_second_of_arc

Question:
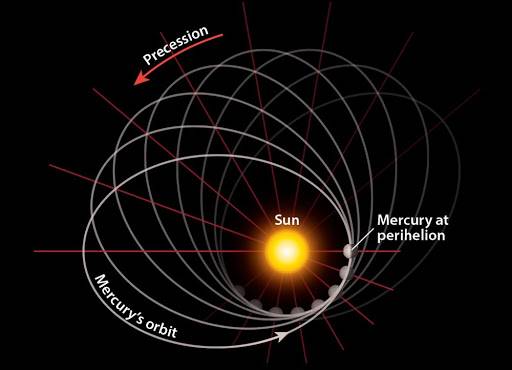
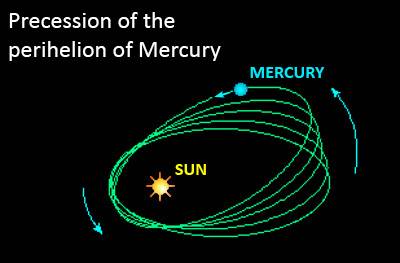
In picture #1 below the orbit is shown precessing counterclockwise and the plane of precessed orbits remains the same. In other words, all the precessed orbits lie in the same plane. But in picture #2 the precession is shown to change the plane of orbits as well. In other words, the precession gives a tilt to orbit along the vertical axis. Or, perhaps it's just me!

I also watched this video and it shows the precession the same way as in picture #2: youtu.be/NXlg3nTqSnk?t=21

Could you please confirm how the orbit of Mercury really precess? Thank you for the help!

Picture #1

Picture #2

 

[Orodruin]

But in picture #2 the precession is shown to change the plane of orbits as well.

The picture does not show this. It is just your interpretation of the picture. Clearly all the picture is in two dimensions and all of the orbits are in the 2D plane of the picture.

 

[Ibix]

I think it's just you - both of those pictures look to me to have the precession in-plane.

Reality is more complicated. First the easy bit: the GR correction you are looking at does not produce any change in orbital plane (although note that this is only true in certain cases - orbits around rapidly spinning black holes can be very complicated). However, the Newtonian prediction of the precession depends on the interaction between Mercury and all other known planets - and they only lie more or less in the same plane. There will be some variation in the orbital plane of each planet as a result.

 

[vanhees71]

In first approximation, where you consider only the Mercury as a test-particle in the Sun's gravitational field (approximately described as a Schwarzschild metric) due to isotropy of the Schwarzschild solution angular momentum is conserved and thus Mercury's orbit a planar orbit. It's very close to a Kepler ellipse you get in the Newtonian theory but with this tiny perihelion shift, which was known before Einstein's GR to astronomers as being not explained by the pertubation of the trajectory due to the presence of other known planets. Thus the first hypothesis was that there may be another unknown planet in the solar system, which however has of course never been found. For Einstein it was one of his most beautiful first results of application of his new theory in 1915 to be able to quantitatively explain this additional perihelion shift which couldn't explained before.

 

[PainterGuy]

Thank you, everyone!

It's very close to a Kepler ellipse you get in the Newtonian theory but with this tiny perihelion shift, which was known before Einstein's GR to astronomers as being not explained by the pertubation of the trajectory due to the presence of other known planets. Thus the first hypothesis was that there may be another unknown planet in the solar system, which however has of course never been found. For Einstein it was one of his most beautiful first results of application of his new theory in 1915 to be able to quantitatively explain this additional perihelion shift which couldn't explained before.

I was only trying to understand it at a basic level and therefore Schwarzschild metric and other terms wouldn't help me much at this level.

Anyway, you are right that the precession of mercury had been calculated carefully well before Einstein's theory of general relativity. To account for the difference between the calculated value and the one predicted by Newton's theory, they came up with mistaken ideas of Vulcan and dust clouds. It was Einstein's theory which gave a final answer.

Personally, I think that when Mercury is closer to the sun, the spacetime gets more warped in the region between it and the sun, and Mercury gets a little bit of an additional amount of 'slide' due to this highly warped spacetime and this amount gets added to the Newtonian theory's predicted value.

Thanks for the help.

 

[PeterDonis]

I think that when Mercury is closer to the sun, the spacetime gets more warped in the region between it and the sun, and Mercury gets a little bit of an additional amount of 'slide' due to this highly warped spacetime and this amount gets added to the Newtonian theory's predicted value.

Are you proposing this as an explanation of the observed GR precession of Mercury's perihelion? If so, it's wrong.

Please review the PF rules about personal speculation.

Thread closed.