The result of a disturbance on an output

[David J]

Homework Statement

[/B]
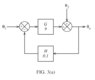
The proportional control system of figure 3(a) (attachment 235263) has an input, $\theta_{1}$, of 10 units. The uncontrolled input, $\theta_{2}$, has a value of 50 units, prior to a step change down to 40 units. The result of this disturbance upon the output, $\theta_{o}$ is shown in figure 3(b) (attachment 235264)

(a) Calculate the change in offset in the output produced by the step change

(b) Draw a modified block diagram to show how the offset could be minimised by the inclusion of another control action. Also, show by means of a sketch how the modification might be expected to affect the output response.

(c) Show, by drawing a modified block diagram, how the magnitude of the disturbance could be minimised by the inclusion of a third type of control action

2. Homework Equations

$\theta_{0}=\frac{\theta_{2} +G\theta_{1}}{1+G}$

The Attempt at a Solution

(a)
[/B]
Prior to the step change

$\theta_{0}$ = $\frac{50 + (9*10)}{1+G}$

so $\theta_{0}$ = $\frac{140}{10}$=$14 m^{3 h-1}$

After the step change

$\theta_{0}$ = $\frac{40 + (9*10)}{1+G}$

so $\theta_{0}$ = $\frac{130}{10}$=$13 m^{3 h-1}$

So in the first instance would I be correct in saying that the change in offset in the output as a result of the step change will be $1 m^{3 h-1}$ ?

I attached some notes, (pages 16 and 17) which I think are in relation to this question

 

[FactChecker]

My approach may be too simple-minded, but the output plot looks like the initial output response is a decrease of 5 units. I don't know what m and h are.

 

[David J]

Hello, the method you see above is the method I was given in my notes but I discovered another way of doing this using laplace transform. The answer from that method was very similar to this which makes me think my answers are close.

The m is for cubic meters but I have just realized that the question does not actually suggest and units so I may be wrong in using $m^{3h-1}$

h is the feedback error I think.

I will post the laplace method in this thread during the next couple of days

 

[FactChecker]

The output response to the $\theta_2$ input is the same as the closed loop response of a negative feedback loop with $G^{\prime} = 1$ and $H^{\prime} = 0.1 * 9 = 0.9$ feedback gain.

 

[David J]

I submitted this and it was marked as correct as per my working out in the first post. The answers to `b` and `c` just required a block diagram showing the addition of the integral action and the derivative action resulting in a block diagram of a PID controller. I will mark this as solved now but if anyone needs any help with this again I can advise.

thanks

 

[Jason-Li]

I submitted this and it was marked as correct as per my working out in the first post. The answers to `b` and `c` just required a block diagram showing the addition of the integral action and the derivative action resulting in a block diagram of a PID controller. I will mark this as solved now but if anyone needs any help with this again I can advise.

thanks

Hi DavidJ again,

Looking at this I don't see how you can't take the H figure into account? I work the formula to have the bottom of the fraction as 1+G*H ?

 

[Jason-Li]

Hello all, for anyone interested in future I started another thread that answers my above query (its not letting me delete my post),

https://www.physicsforums.com/threads/disturbance-in-a-proportional-control-system.998338/

Thanks