- 1,255
- 1,058
It is just for teaching experience sharing. Consider a uniform disk. A stretchless and massless wire has been wound on the disk. The end of the wire is attached to the ceiling. Initially the system is at rest as it is shown at the picture. Then the disk is released. It falls down and rotates and the wire unwinds.
Prove that the unwound part of the wire keeps being vertical for all the time.
This fact is evident (I do not know why), nevertheless to provide a correct proof one must write the Lagrange equations for the system with two degrees of freedom and make sure that the corresponding motion satisfies the equations.
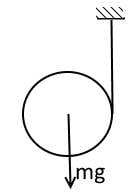
Prove that the unwound part of the wire keeps being vertical for all the time.
This fact is evident (I do not know why), nevertheless to provide a correct proof one must write the Lagrange equations for the system with two degrees of freedom and make sure that the corresponding motion satisfies the equations.
Last edited: