The Vertical Force of a Spring: A Logical Argument

[sysprog]

No, in the absence of gravity A and C would be the same point.

That's a definitional difference. The mass rotates about point $\text A$ in either case. Removing the gravity would make the rotation about point $\text A$ circular with the center at point $\text A$, instead of the rotation being circular about the point formerly called point $\text C$. In discussing the effect of removing gravity, I regarded point $\text C$ as a static point already defined as in the original problem. You're using a dynamic definition of point $\text C$ to mean the center of the circle of rotation, wherever that is. The effect of removing gravity is the same by either description.

 

[haruspex]

That's a definitional difference. The mass rotates about point $\text A$ in either case. Removing the gravity would make the rotation about point $\text A$ circular with the center at point $\text A$, instead of the rotation being circular about the point formerly called point $\text C$. In discussing the effect of removing gravity, I regarded point $\text C$ as a static point already defined as in the original problem. You're using a dynamic definition of point $\text C$ to mean the center of the circle of rotation, wherever that is. The effect of removing gravity is the same by either description.

In post #65 you wrote "... rather than about C", implying it would not be about C. I merely pointed out that in the absence of gravity, by definition of those points, A and C wouid be the same point. Thus, the correct way to view it is that the rotation always centres on C.

 

[hutchphd]

But I know you argued that it suffices to use the info that the motion is circular. I can see that in principle that may do it, but I am afraid I still haven’t understood how your argument works. Maybe take that into a private discussion.

What I said was much stronger than that and much simpler. With a simple change in origin, the equations of motion have complete circular symmetry and no longer contain the gravity constant g.

What is there to discuss? (If I seem vexed it is because I am! This is just a simple truth. If you feel the need to describe the springs in gory detail then OK we can do that but it cannot change the result)

 

[sysprog]

In post #65 you wrote "... rather than about C", implying it would not be about C. I merely pointed out that in the absence of gravity, by definition of those points, A and C wouid be the same point. Thus, the correct way to view it is that the rotation always centres on C.

What I said meant that it would no longer be about point $\text C$, by which I meant the point about which mass $\text P$ would rotate circularly in the presence of gravity. That point would still exist without gravity, and I didn't change its label in referencing it as no longer the center of the circular rotation once gravity is removed. I could have called it e.g. 'point $\text C_{old}$', but I think that which point I meant was not unclear.

 

[sysprog]

What I said was much stronger than that and much simpler. With a simple change in origin, the equations of motion have complete circular symmetry and no longer contain the gravity constant g.

What is there to discuss? (If I seem vexed it is because I am! This is just a simple truth. If you feel the need to describe the springs in gory detail then OK we can do that but it cannot change the result)

In SHM the velocity constantly varies, unlike in uniform circular motion. I alluded to the variation in velocity in post #21, without using the term 'SHM' (I said that the variation in velocity of the rotation would be sinusoidally periodic). I think that strictly uniform rotation is not present, and that the constancy of the period and frequency suffices, along with the problem statement, to justify the argument in sentences 1 and 2 of the given solution.

From: https://en.wikipedia.org/wiki/Simple_harmonic_motion:

(edited to freeze the animation)

No-one who has done (or even witnessed) a bungee cord jump would suppose that the velocity is constant, but some might be surprised that the period and frequency are (ideally) constant

 

[haruspex]

What I said was much stronger than that and much simpler. With a simple change in origin, the equations of motion have complete circular symmetry and no longer contain the gravity constant g.

What is there to discuss? (If I seem vexed it is because I am! This is just a simple truth. If you feel the need to describe the springs in gory detail then OK we can do that but it cannot change the result)

My difficulty with that is that without the fact that the string has zero relaxed length the result to be proved is false. Therefore one must make use of that info about the string, either directly or indirectly. An indirect usage might be by using that the trajectory is circular, but I am not seeing how that swiftly leads to constant speed.

 

[haruspex]

In SHM the velocity constantly varies, unlike in uniform circular motion.

It is SHM in each coordinate independently. Given the same amplitude and frequency but 90 degrees phase separation, the velocities are of the form $v\sin(\omega t)$ and $v\cos(\omega t)$. The speed is therefore v, always: uniform circular motion.

 

[hutchphd]

My difficulty with that is that without the fact that the string has zero relaxed length the result to be proved is false.

But relaxed length is not force equilibrium when there is gravity. Equilibrium is at -mg/k.
Also the equations cannot lie and they know about the spring length!...don't know what else to say.

 

[haruspex]

But relaxed length is not force equilibrium when there is gravity. Equilibrium is at -mg/k.
Also the equations cannot lie and they know about the spring length!...don't know what else to say.

We might be able to resolve this if you post your actual equations.

 

[hutchphd]

I will practice my Latex on you tomorrow...I'm done for the evening. I promise 4 lines at most...look forward to it.
Do you stipulate that the 2D isotropic SHO without gravity is good and well behaved with respect to the issues in question?

 

[haruspex]

Do you stipulate that the 2D isotropic SHO without gravity is good and well behaved with respect to the issues in question?

Not sure what you are asking, but the no gravity case is different because it does not depend on the zero relaxed length.

 

[hutchphd]

As requested:

The equation of motion for the position r(t) of the mass without gravity is $$m\ddot {\mathbf r}+
k\mathbf r=\mathbf 0$$
Notice this describes a spring of zero unstretched length. If we put gravity in then the equation for R(t) contains the force
$$m\ddot {\mathbf R}+k\mathbf R=m\mathbf g$$
This still describes a spring of zero unstretched length.
Notice that any solution r(t) of the first (homogeneous) equation gives rise to a corresponding solution R(t) of the second (inhomogeneous) equation (and vice versa) $$\mathbf R=\mathbf r+\frac m k \mathbf g$$
and of course $$\mathbf { \dot R =\dot r}$$and $$\mathbf { \ddot R =\ddot r}$$
QED.

 

[haruspex]

As requested:

The equation of motion for the position r(t) of the mass without gravity is $$m\ddot {\mathbf r}+
k\mathbf r=\mathbf 0$$
Notice this describes a spring of zero unstretched length. If we put gravity in then the equation for R(t) contains the force
$$m\ddot {\mathbf R}+k\mathbf R=m\mathbf g$$
This still describes a spring of zero unstretched length.
Notice that any solution r(t) of the first (homogeneous) equation gives rise to a corresponding solution R(t) of the second (inhomogeneous) equation (and vice versa) $$\mathbf R=\mathbf r+\frac m k \mathbf g$$
and of course $$\mathbf { \dot R =\dot r}$$and $$\mathbf { \ddot R =\ddot r}$$
QED.

Ok, fine, but this just looks like a vector representation of the same method I outlined. And you are using the zero relaxed length, which was not clear in your earlier posts.
We are in violent agreement.

 

[sysprog]

Tension on the spring points inward from the circle to its center, while the gravity always points downward.

If the weight is moving counter-clockwise:

then on the left side of the circle, $$\frac {v^2}r=\frac{mg+T}m,$$so$$T=m\frac{v^2}r−mg,$$ and on the right side of the circle, $$\frac{v^2}r=−\frac{mg+T}m,$$so$$T=\frac{mv^2}r+mg.$$The spring alternates between storing the acceleration of gravity on the downward part of the circular path, and restoring it compensatorily on the upward part of the circular path.

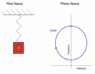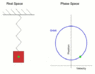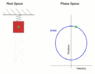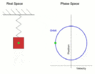
let be $\vec r$ the position vector of the particle. A the spring has zero relaxed length, the spring force is $-k \vec r$. the total force also includes gryvity. WE set the coordinate system with horizontal x-axis and vertical down y axis.

The vertical axis would not be restricted to 'down' only, but the gravity is always downward.

The equation of motion in coordinates is
$m\ddot x=−kx$
$m\ddot y=−ky+mg$

Given that $k$ is always directed along $\vec r$ toward the center, while $mg$ is always directed down, the $\ddot y$ acceleration of $mg$ alternates between
$m\ddot y=−ky+mg$
and
$m\ddot y=−ky−mg$.

This is a linear , constant coeffient, inhomogeneous DE. the solution of the homogeneous part is a two-dimensional vibration with angular frequancy
$ω=k/m$ A particular solution of the inhomogeneous equation is $h=mg/k$ that corresponds to the steady state.

For the new variables $X=x$ and $Y= y-h$, the differential equation becomes $m\ddot X=−kX$ and $m\ddot Y=−kY$. The solution can be a circular motion with angular frequeny $ω=\frac k m$, and arbitrary radius $R$. Then the speed is constant, $ωR$.
The problem maker might have took that straightforward, when assuming constant speed.

No basis is shown for assuming constant speed.

Given only the spring force, gravity, and from an initial static state at the equilibrium point an external initial tangential impetus sufficient to incipiate rotation, I think that the speed component of the angular velocity $\omega$, although it would be of a constant frequency and period, would vary within the cycle, increasing in the left semicircle, and decreasing in the right, with $v_{max}$ at the lowest point, $v_{min}$ at the highest, and $v_{mean}$ at the two exactly vertical exorbital tangent points, downward and upward, at the leftmost and rightmost points, respectively.

The rightmost of these is the one that the problem recipient is in the solution asked to consider, and it is in my view sufficient for purposes of the argument that this point has the mean vertical velocity; the velocity is not, and need not be, constant throughout the cycle.

If there's something that I'm missing it wouldn't be the first time.

@berkeman: A minor edit produced $LaTeX$ rendering failure -- post-edit preview was fine, but upon save, no rendering . . . the only change made was from $vec r$ to $\vec r$ . . . (now fixed, thanks) (oops . . . editing to acknowledge the fix and say thanks broke it again)

 

[hutchphd]

If there's something that I'm missing it wouldn't be the first time.

If I understand your description, your concept is incorrect.
For either the gravity or no gravity case, if the mass starts at equilibrium and at rest and is imparted a horizontal impulse, it will oscillate in a line horizontally. The vertical velocity will be zero. Period.

 

[ehild]

Tension on the spring points inward from the circle to its center, while the gravity always points downward.

If the weight is moving counter-clockwise:

then on the left side of the circle, $$\frac {v^2}r=\frac{mg+T}m,$$so$$T=m\frac{v^2}r−mg,$$ and on the right side of the circle, $$\frac{v^2}r=−\frac{mg+T}m,$$so$$T=\frac{mv^2}r+mg.$$The spring alternates between storing the acceleration of gravity on the downward part of the circular path, and restoring it compensatorily on the upward part of the circular path.
The vertical axis would not be restricted to 'down' only, but the gravity is always downward.
Given that $k$ is always directed along $vec r$ toward the center, while $mg$ is always directed down, the $\ddot y$ acceleration of $mg$ alternates between
$m\ddot y=−ky+mg$
and
$m\ddot y=−ky−mg$.

This is not right. The force of gravity always causes downward acceleration, and the spring force causes acceleration opposite to the displacement.
$m\ddot y=−ky+mg$ is true
$m\ddot y=−ky−mg$. is false.

No basis is shown for assuming constant speed.

The equations for the x and y coordinates
$m\ddot y=−ky+mg$
$m\ddot x=−kx$
ensure circular motion with constant speed, see Posts #61 and #82 for example. A constant external force does not make vary the vibrational frequency of a string-mass system, and if that motion is circular, the speed is constant.

 

[sysprog]

If I understand your description, your concept is incorrect.
For either the gravity or no gravity case, if the mass starts at equilibrium and at rest and is imparted a horizontal impulse, it will oscillate in a line horizontally. The vertical velocity will be zero. Period.

How then does the trajectory get to be circular, as in the drawing in the problem description? $-$ this version has the original, along with @TSny's vector diagram (which has $\vec h$, where the original drawing has $h$ next to a $\updownarrow$ segment), and my syncresis from those two renditions $-$ I think that at point $\delta$ a tangential acceleration would be horizontal, and the spring tension is orthogonal to, not diametrically oppositional to, the horizontal exorbital tangent, and so coerces orbital, rather than linear, trajectory.

 

[haruspex]

How then does the trajectory get to be circular, as in the drawing in the problem description? $-$ this version has the original, along with @TSny's vector diagram (which has $\vec h$, where the original drawing has $h$ next to a $\updownarrow$ segment), and my syncresis from those two renditions $-$ I think that at point $\delta$ a tangential acceleration would be horizontal, and the spring tension is orthogonal to, not diametrically oppositional to, the horizontal exorbital tangent, and so coerces orbital, rather than linear, trajectory.

View attachment 267098

At point δ there are no horizontal forces, so no tangential acceleration.
I didn't understand the last bit, about linear trajectory. Are you arguing against circular motion now or against the special case of linear reciprocating motion that @TSny mentions?

 

[hutchphd]

With sincere apologies I again don't even know what the question is. Is it "how do you make circular motion??"
This is a simple system that is essentially the same whether there is gravity or not. The result of a given external force sequence will produce identical subsequent motion in either case (from equilibrium... gravity or not). If I knew what the question was I would supply the explicit solution to you in half a page.
I am mystified as to what is left unknown...after 66 posts...

 

[sysprog]

I'm grateful to @haruspex, @hutchphd, @TSny, @ehild, for responding to my meanderings regarding this matter, and to @guv for posing the problem and commenting regarding the responses.

When I was earlier today at the grocery store, although I was trying to be not too conspicuous, despite my desperado-style SARS-II COVID-19 kerchief, I went to the brink of consternating one or two members of the staff, by conducting a few crude experiments with the produce scale, which looked pretty much like this:

The one there was branded Ohaus, but it looked pretty similar otherwise. It had an attached ring (not present in the image here presented) above the 0 numeral, by which it was hanging from a hook attached to a substantially heavy steel frame.

The results of my necessarily overly hasty experiments confirmed nothing firmly, except that when I pushed and held mostly horizontally and somewhat upward at the U-shaped fixture below the $\text 5$ numeral, the red needle continued to point pretty much straight up, so that it was indicating a little below the $\text 9$ numeral on the scale, and that result was not inconsistent with my surmises regarding the tension and the effects of gravity and of opposition thereto thereon.

I think that my hope that I won't have to resort to doing second derivatives and definite integrals to try to clarify or justify, even to myself, what I've already said here about the velocity may be in vain.

 

[hutchphd]

Alas I miss the grocery store...

This colloquy has seemed to me a prime example of the pitfalls of doing physics without formal maths
In particular, as I have mentioned,

surmises regarding the tension and the effects of gravity and of opposition thereto thereon.

I still do not know what the surmises are or even their number. So much the pity, because I feel that some of the results you to which you allude may not be correct; the formal approach in this case is actually simpler and my intuition alone would not necessarily get me to the correct result. It is a case study in method.
I have been mildly frustrated because it is impossible to provide an answer (even when known) if you cannot ascertain the specific question!
But a good time was had by all...

 

[sysprog]

Alas I miss the grocery store...

This colloquy has seemed to me a prime example of the pitfalls of doing physics without formal maths
In particular, as I have mentioned,

I still do not know what the surmises are or even their number. So much the pity, because I feel that some of the results you to which you allude may not be correct; the formal approach in this case is actually simpler and my intuition alone would not necessarily get me to the correct result. It is a case study in method.
I have been mildly frustrated because it is impossible to provide an answer (even when known) if you cannot ascertain the specific question!
But a good time was had by all...

Whence the rotation?

 

[hutchphd]

Whence the rotation?

initial conditions: For instance horizontal impulse followed by vertical impulse a quarter period π/2ω iater...or pull it off equilibrium sideways and give it the appropriate vertical speed...or give it a tangent spiral in an initial interval.
The circle is certainly an allowed solution whatever the size of gravity.

 

[sysprog]

initial conditions: For instance horizontal impulse followed by vertical impulse a quarter period π/2ω iater...or pull it off equilibrium sideways and give it the appropriate vertical speed...or give it a tangent spiral in an initial interval.
The circle is certainly an allowed solution whatever the size of gravity.

Why would both the radius of the circle and also the velocity of the weight be invariant within the cycle whatever the varying direction of the weight within the cycle with respect to the invariant direction of the gravity?

 

[haruspex]

Why would both the radius of the circle and also the velocity of the weight be invariant within the cycle whatever the varying direction of the weight within the cycle with respect to the invariant direction of the gravity?

Because when you do the math, which you have conspicuously failed to do, you find that, given the right initial conditions, the resultant of the tension in the string and gravity is of constant magnitude and is always normal to the velocity.

 

[hutchphd]

Why would both the radius of the circle and also the velocity of the weight be invariant within the cycle whatever the varying direction of the weight within the cycle with respect to the invariant direction of the gravity?

I think it is intuitive that this is possible in the absence of gravity (yes?). It certainly is easy to show also.
It has been shown almost trivially (see #83 ) the solution with gravity is identical in shape and speed and acceleration to the no gravity one.
Therefore it is absolutely true. One need not look farther.

 

[haruspex]

conducting a few crude experiments with the produce scale,

The hard part about demonstrating the result experimentally is the zero relaxed length condition. One way would be with a torsion spring on a horizontal axis connected to the axle of a drum. A string is wound around the drum. Just where the string leaves the drum, at the same height as its axis, it passes through a small smooth aperture, to prevent sideways movement, then, with the torsion spring in its relaxed state, connects immediately to the mass.
Thus, the distance of the mass from the aperture is proportional to the angle of torsion on the spring.

 

[hutchphd]

Its tricky to get an exact circle even if the springs have a nonzero outstretched length. Why is it easier for the nonzero case?
Seems to me the method usually used is to displace the object radially outward and then supply just the right amount of tangential velocity (pull it out and shove it sideways).

The astronauts get to make corrective burns to circularize their orbits...

 

[kuruman]

I am a latecomer to this thread, but there is a simple heuristic way to look at this by bringing two considerations together.

First, a vertical spring-mass system in gravity behaves as a horizontal spring-mass system with the equilibrium position lowered to $\dfrac{mg}{k}$ from the relaxed position.
In this case the position of the mass relative to the relaxed position can be written as $$y(t) =A\cos(\omega t)-\frac{mg}{k}.$$ The initial conditions are $y(0)=A-\dfrac{mg}{k}~;~~\dot y(0)=0.$

Second, a mass, undergoing uniform circular motion in the $xy$-plane of radius $A$ with angular speed $\omega$, has coordinates $$x(t)=A\sin(\omega t)~;~~y(t)=A\cos(\omega t).$$ That's for a line of sight along the $z$-axis. If viewed along the $x$-axis the motion is the same (mathematically) as that of a spring-mass system oscillating along the $y$-axis such that $\sqrt{\frac{k}{m}}$ matches the angular speed of the circular motion.

Putting the two considerations together, we can immediately write an expression for the position of the mass$$\vec r(t)=A\sin(\omega t)~\hat x+\left(A\cos(\omega t)-\frac{mg}{k}\right)~\hat y.$$We can verify that this works with a parametric plot ($A=1;~mg/k=A/3$)

Clearly, $$\ddot x =-\omega^2 x~;~~\ddot y=-\omega^2 y$$which are the equations of motion for a spring of zero length placed at the origin of Cartesian coordinates. Thus, we have a solution that is consistent with Newton's second law. Initial conditions and anything else one cares to find can be obtained from $\vec r(t)$. Finally, I see no reason why this cannot be extended to a sphere in three dimensions.