Thermodynamic functions and state variables

[cianfa72]

Hi,

a basic doubt about thermodynamic functions and state variables. Take for instance transformations I and II in the following $(p,V)$ plane.

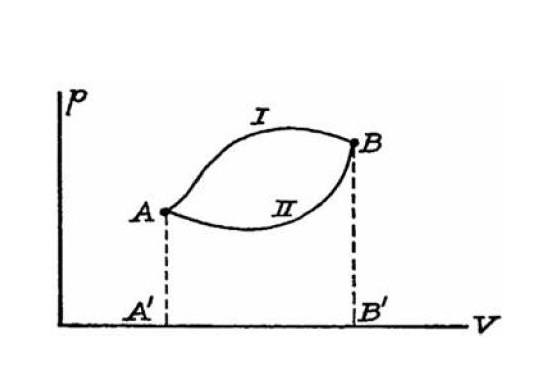
As far as I can tell, just because the transformations are drawn as continuous lines they are reversible by definition. Namely we can transform the system back in the other way and from a mathematical point of view it really makes sense (e.g. work and heat exchanged with the system's surrounding are the same as in the 'direct' transformation just with sign flipped).

By the way, given a system (e.g. a gas in a cylinder), there exist a pair of state variables for each way the system can exchange energy with the surrounding. In the above case the system can do work by means of gas thermodynamic pressure $p$ and exchange heat with the surrounding. Hence we have 2 pairs: $(p,V)$ and $(t,S)$ respectively.

Now my point is: how many are the independent state variables ?

The 'state equation' for the system involves the variables $p,V,t$ (take for instance the state equation of ideal gas) and I believe there exist another independent equation that involve the entropy $S$. Thus in that case (system = gas in a cylinder) the independent state variables are just 2.

Does it makes sense ? Thank you.

Note: In the above I use lower case for intensive state variables and upper case the extensive ones.

 

[Chestermiller]

If you are talking about a single phase gas of constant composition and believe the Phase Rule, it tells us that there are two independent state variables.

 

[cianfa72]

If you are talking about a single phase gas of constant composition and believe the Phase Rule, it tells us that there are two independent state variables.

Yes, assume a single phase gas of constant composition (and believe in the Phase Rule).

Sorry, I didn't get your point: is the Phase Rule actually another 'state equation' relating the system's state variables $p,V,t,S$ ?

 

[Chestermiller]

Yes, assume a single phase gas of constant composition (and believe in the Phase Rule).

Sorry, I didn't get your point: is the Phase Rule actually another 'state equation' relating the system's state variables $p,V,t,S$ ?

Google Gibbs Phase Rule.

 

[cianfa72]

From a mathematical point of view, we can employ the 'contact manifold' geometry to represent a thermodynamic system (material/substance). Basically it is a 5D manifold endowed with a contact structure -- Contact geometry

This contact structure represents the thermodynamic first law:

$$ dU - TdS - pdV = 0 $$
$d\omega = dU - TdS - pdV$ is the one-form contact structure defined on the 5D manifold. Each material/substance is actually represented by a 2D submanifold of it.

Basically the constrains between the 5 state variables $(U,S,V,T,p)$ define such submanifold and some of them are actually the 'state equations' for the given substance.

See the following:
thermodynamic formalism
MathThermoStates

 

[Chestermiller]

From a mathematical point of view, we can employ the 'contact manifold' geometry to represent a thermodynamic system (material/substance). Basically it is a 5D manifold endowed with a contact structure -- Contact geometry

This contact structure represents the thermodynamic first law:

$$ dU - TdS - pdV = 0 $$
$d\omega = dU - TdS - pdV$ is the one-form contact structure defined on the 5D manifold. Each material/substance is actually represented by a 2D submanifold of it.

Basically the constrains between the 5 state variables $(U,S,V,T,p)$ define such submanifold and some of them are actually the 'state equations' for the given substance.

See the following:
thermodynamic formalism
MathThermoStates

I have no idea what any of this means, and, in my scheme of things (focused on solving actual problems), it doesn't matter.

 

[cianfa72]

Yes, mine was a theoretical approach to address the following: taking for instance the 'ideal gas substance' why its state can be described by just 2 state variables picked from the set of 5 state variables above ?

 

[vanhees71]

It should of course read
$$\mathrm{d} U-T \mathrm{d} S + P \mathrm{d} V=0.$$
Otherwise it's just the geometric intuition behind all the many Legendre transformations you do to transform from one thermodynamic potential to the other.

 

[cianfa72]

It should of course read
$$\mathrm{d} U-T \mathrm{d} S + P \mathrm{d} V=0.$$

Oops, yes of course.