- #1
zenterix
- 480
- 70
- TL;DR Summary
- Different books seem to say different things about the calculation of work of a hydrostatic system contained in a cylinder with a frictionless massless piston that is used to compress or expand the volume of the system in various ways.
I'd like to show two different ways of defining work in a hydrostatic (PVT) system in a cylinder with a piston.
One way is in a book that I have slowly come to hate: Physical Chemistry by Silbey, Alberty, and Bawendi.
In that book, work is defined using the external pressure on the piston
$$dW = -P_{ext}dV$$
In one section they consider an idealized scenario of constant temperature (the cylinder is immersed in a thermostat at constant temperature T) and add a constant external pressure ##P_2## on the piston (some specific mass placed on top of the piston) that is larger than the internal pressure ##P_1##, and starting at some ##V_1## the gas is thus compressed until the volume is at the smaller ##V_2## at a new higher internal pressure ##P_2##
##-P_{2}(V_2-V_2)##, which is positive, is the "smallest amount of work that can be used to compress a gas from ##V_i## to ##V_f## in a single step at constant temperature.
Here are depictions of this
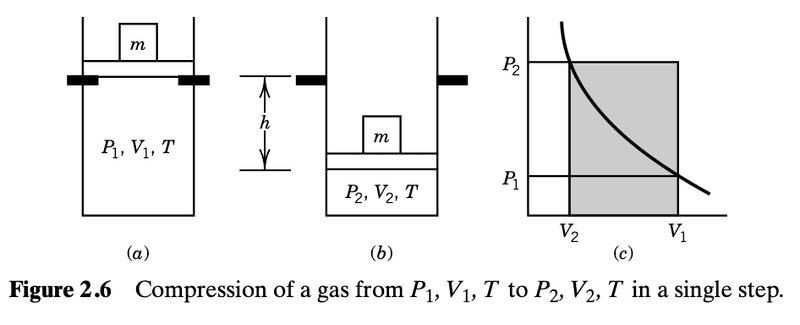
They don't consider the case where you use a very small mass on top of the piston but it seems analogous. We'd have an expansion. If we try to visualize this in the context of the pictures above, we start at ##P_2, V_2, T## and we end up at ##P_1, V_1, T##, where ##P_{ext}=P_1##.
The work done is now the area ##-P_1(V_1-V_2)<0##.
If we consider the scenario where we have no external pressure, then the work would be zero.
Okay, now I want to make a few comments based on a book that I have quickly come to love: Heat and Thermodynamics by Zemansky and Dittman.
Let's imagine once again a hydrostatic system in a closed cylinder equipped with a frictionless massless movable piston on which the system and its surroundings may act (note that we could use any shape for the closed container containing the system; the important thing is the setup where we can expand and contract the hydrostatic system contained within).
The cylinder has a cross-sectional area A and the pressure exerted by the system at the piston face is P.
The force on the internal face of the piston is therefore PA.
The surroundings may exert an opposing force on the piston. The origin of this force is irrelevant from the point of view of the hydrostatic system in the cylinder.
As long as the difference between the two forces on the piston is small enough, we may be able to obtain a change in the position of the piston in a way that can be described using the equation of state of the hydrostatic system.
We need to be able to say that there is a uniform pressure in the system. If the system moves too fast this is no longer true: for example, if there is turbulence or waves in the system due to rapid expansion or compression of the piston, then the pressure in the system is variable depending on the point or region of the system you are considering.
Assuming that the above assumptions are met (there is mechanical equilibrium of the system and the difference in forces is infinitesimal) then the work that will be done by or on the system can be described using equations of state at each intermediate step of the process.
From the definition of work, pressure, and infinitesimal change in volume we have
$$dW=Fdx=PAdx=PdV$$
If we leave things like this then between two equilibrium states we have
$$dW=\int_{V_i}^{V_f} PdV$$
Which gives us positive work when ##V_f>V_i## and vice-versa.
However, in thermodynamics, the convention is that we should have ##negative work## in this case of ##V_f>V_i##, ie expansion, and positive work in the case of compression.
Thus, the convention is that ##Adx=-dV## and so
$$dW=-\int_{V_i}^{V_f} PdV$$
Now, this integral is path dependent (ie, it depends on the intermediate states of equilibrium). Since ##P## is a function of both ##V## and ##T##,
But my main point here is to say that the concept of work is the same as in mechanics, it's just that we now have a more complicated function that isn't conservative.
What happens if there is no external force on the piston?
As far as I understand from the theory presented in this book, there is also no possible calculation of work at all because there is no single pressure to speak of as the system expands.
I am interested to know if the approaches to this topic used in these two books is in fact different or if it is just my impression?
One way is in a book that I have slowly come to hate: Physical Chemistry by Silbey, Alberty, and Bawendi.
In that book, work is defined using the external pressure on the piston
$$dW = -P_{ext}dV$$
In one section they consider an idealized scenario of constant temperature (the cylinder is immersed in a thermostat at constant temperature T) and add a constant external pressure ##P_2## on the piston (some specific mass placed on top of the piston) that is larger than the internal pressure ##P_1##, and starting at some ##V_1## the gas is thus compressed until the volume is at the smaller ##V_2## at a new higher internal pressure ##P_2##
##-P_{2}(V_2-V_2)##, which is positive, is the "smallest amount of work that can be used to compress a gas from ##V_i## to ##V_f## in a single step at constant temperature.
Here are depictions of this
They don't consider the case where you use a very small mass on top of the piston but it seems analogous. We'd have an expansion. If we try to visualize this in the context of the pictures above, we start at ##P_2, V_2, T## and we end up at ##P_1, V_1, T##, where ##P_{ext}=P_1##.
The work done is now the area ##-P_1(V_1-V_2)<0##.
If we consider the scenario where we have no external pressure, then the work would be zero.
Okay, now I want to make a few comments based on a book that I have quickly come to love: Heat and Thermodynamics by Zemansky and Dittman.
Let's imagine once again a hydrostatic system in a closed cylinder equipped with a frictionless massless movable piston on which the system and its surroundings may act (note that we could use any shape for the closed container containing the system; the important thing is the setup where we can expand and contract the hydrostatic system contained within).
The cylinder has a cross-sectional area A and the pressure exerted by the system at the piston face is P.
The force on the internal face of the piston is therefore PA.
The surroundings may exert an opposing force on the piston. The origin of this force is irrelevant from the point of view of the hydrostatic system in the cylinder.
As long as the difference between the two forces on the piston is small enough, we may be able to obtain a change in the position of the piston in a way that can be described using the equation of state of the hydrostatic system.
We need to be able to say that there is a uniform pressure in the system. If the system moves too fast this is no longer true: for example, if there is turbulence or waves in the system due to rapid expansion or compression of the piston, then the pressure in the system is variable depending on the point or region of the system you are considering.
Assuming that the above assumptions are met (there is mechanical equilibrium of the system and the difference in forces is infinitesimal) then the work that will be done by or on the system can be described using equations of state at each intermediate step of the process.
From the definition of work, pressure, and infinitesimal change in volume we have
$$dW=Fdx=PAdx=PdV$$
If we leave things like this then between two equilibrium states we have
$$dW=\int_{V_i}^{V_f} PdV$$
Which gives us positive work when ##V_f>V_i## and vice-versa.
However, in thermodynamics, the convention is that we should have ##negative work## in this case of ##V_f>V_i##, ie expansion, and positive work in the case of compression.
Thus, the convention is that ##Adx=-dV## and so
$$dW=-\int_{V_i}^{V_f} PdV$$
Now, this integral is path dependent (ie, it depends on the intermediate states of equilibrium). Since ##P## is a function of both ##V## and ##T##,
But my main point here is to say that the concept of work is the same as in mechanics, it's just that we now have a more complicated function that isn't conservative.
What happens if there is no external force on the piston?
As far as I understand from the theory presented in this book, there is also no possible calculation of work at all because there is no single pressure to speak of as the system expands.
I am interested to know if the approaches to this topic used in these two books is in fact different or if it is just my impression?
Last edited: